
【題目】在Rt△ABC中,AB=AC,D為BC邊上一點(不與點B,C重合),將線段AD繞點A逆時針旋轉90°得到AE.
(1)連接EC,如圖①,試探索線段BC,CD,CE之間滿足的等量關系,并證明你的結論;
(2)連接DE,如圖②,求證:BD2+CD2=2AD2
(3)如圖③,在四邊形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=![]() ,CD=1,則AD的長為 ▲ .(直接寫出答案)
,CD=1,則AD的長為 ▲ .(直接寫出答案)

【答案】(1)BC=DC+EC,理由見解析;(2)見解析;(3)![]()
【解析】
(1)根據本題中的條件證出△BAD≌△CAE(SAS), 得到BD=CE,再根據條件即可證出結果.
(2)由(1)中的條件可得∠DCE=∠ACE+∠ACB=90°, 所以CE2+CD2=ED2,可推出BD2+CD2=![]() ,再根據勾股定理可得出結果.
,再根據勾股定理可得出結果.
(3)作AE⊥AD,使AE=AD,連接CE,DE,可推出△BAD≌△CAE(SAS),所以BD=CE=![]() ,再根據勾股定理求得DE.
,再根據勾股定理求得DE.
解:(1)結論:BC=DC+EC
理由:如圖①中,
∵∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
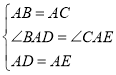 ,
,
∴△BAD≌△CAE(SAS);
∴BD=CE,
∴BC=BD+CD=EC+CD,
即:BC=DC+EC.
(2)BD2+CD2=2AD2,
理由如下:連接CE,
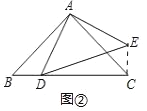
由(1)得,△BAD≌△CAE,
∴BD=CE,∠ACE=∠B,
∴∠DCE=∠ACE+∠ACB=90°,
∴CE2+CD2=ED2,
即:BD2+CD2=ED2;
在Rt△ADE中,AD2+AE2=ED2,又AD=AE,
∴ED2=2AD2;
∴BD2+CD2=2AD2;
(3)AD的長為![]() (學生直接寫出答案).
(學生直接寫出答案).
作AE⊥AD,使AE=AD,連接CE,DE,

∵∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD與△CAE中,
AB=AC,∠BAD=∠CAE,AD=AE.
∴△BAD≌△CAE(SAS),
∴BD=CE=![]() ,
,
∵∠ADC=45°,∠EDA=45°,
∴∠EDC=90°,
∴DE2=CE2-CD2=(![]() )2-12=12,
)2-12=12,
∴DE=2![]() ,
,
∵∠DAE=90°,AD2+AE2=DE2,
∴AD=![]() .
.


科目:初中數學 來源: 題型:
【題目】某學校在疫情期間的復學準備工作中,為了貫徹落實“生命重于泰山,安全至關重要”的思想,計劃購買室內、室外兩種型號的消毒液.已知每桶室外消毒液的價格比每桶室內消毒液的價格多30元,買2桶室內消毒液和3桶室外消毒液共需340元.
(1)求室內、室外兩種型號消毒液每桶的價格;
(2)根據學校實際情況,需購買室內、室外兩種型號的消毒液共200桶,總費用不高于1.4萬元,問室內消毒液至少要購買多少桶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC的內切圓⊙O與兩直角邊AB、BC分別相切于點D、E,過劣弧![]() (不包括端點D、E)上任一點作⊙O的切線MN與AB、BC分別交于點M、N.若⊙O的半徑為r,則Rt△MBN的周長為( )
(不包括端點D、E)上任一點作⊙O的切線MN與AB、BC分別交于點M、N.若⊙O的半徑為r,則Rt△MBN的周長為( )

A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
查看答案和解析>>
科目:初中數學 來源: 題型:
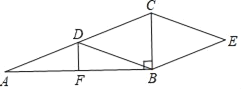
【題目】如圖,Rt△ABC中,∠ABC=90°,點D,F分別是AC,AB的中點,CE∥DB,BE∥DC.
(1)求證:四邊形DBEC是菱形;
(2)若AD=3,DF=1,求四邊形DBEC面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,等邊![]() 的頂點
的頂點![]() 在
在![]() 軸的負半軸上,點
軸的負半軸上,點![]() 的坐標為
的坐標為![]() ,則點
,則點![]() 坐標為_______;點
坐標為_______;點![]() 是位于
是位于![]() 軸上點
軸上點![]() 左邊的一個動點,以
左邊的一個動點,以![]() 為邊在第三象限內作等邊
為邊在第三象限內作等邊![]() ,若點
,若點![]()
![]() .小明所在的數學興趣合作學習小組借助于現代互聯網信息技術,課余時間經過探究發現無論點
.小明所在的數學興趣合作學習小組借助于現代互聯網信息技術,課余時間經過探究發現無論點![]() 在點
在點![]() 左邊
左邊![]() 軸負半軸任何位置,
軸負半軸任何位置,![]() ,
,![]() 之間都存在著一個固定的一次函數關系,請你寫出這個關系式是_____.
之間都存在著一個固定的一次函數關系,請你寫出這個關系式是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利達經銷店為某工廠代銷一種建筑材料(這里的代銷是指廠家先免費提供貨源,待貨物售出后再進行結算,未售出的由廠家負責處理).當每噸售價為260元時,月銷售量為45噸.該經銷店為提高經營利潤,準備采取降價的方式進行促銷.經市場調查發現:當每噸售價每下降10元時,月銷售量就會增加7.5噸.綜合考慮各種因素,每售出一噸建筑材料共需支付廠家及其它費用100元.設每噸材料售價為x(元),該經銷店的月利潤為y(元).
(1)當每噸售價是240元時,計算此時的月銷售量;
(2)求出y與x的函數關系式(不要求寫出x的取值范圍);
(3)該經銷店要獲得最大月利潤,售價應定為每噸多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為表彰在某活動中表現積極的同學,老師決定購買文具盒與鋼筆作為獎品.已知5個文具盒、2支鋼筆共需100元;3個文具盒、1支鋼筆共需57元.
(1)每個文具盒、每支鋼筆各多少元?
(2)若本次表彰活動,老師決定購買10件作為獎品,若購買![]() 個文具盒,10件獎品共需
個文具盒,10件獎品共需![]() 元,求
元,求![]() 與
與![]() 的函數關系式.如果至少需要購買3個文具盒,本次活動老師最多需要花多少錢?
的函數關系式.如果至少需要購買3個文具盒,本次活動老師最多需要花多少錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com