Question

設函數y＝kx²＋(2k＋1)x＋1(k為實數)．
【小題1】寫出其中的兩個特殊函數，使它們的圖象不全是拋物線，并在同一直角坐標系中用描點法畫出這兩個特殊函數的圖象
【小題2】根據所畫圖象，猜想出：對任意實數k，函數的圖象都具有的特征，并給予證明
【小題3】對任意負實數k，當x<m時，y隨著x的增大而增大，試求出m的一個值

Answer 1

【小題1】當k=1時，y= x²＋3x+1;當k=0時y="x+1," 圖象略
【小題2】見解析
【小題3】只要m的值不大于-1即可

解析（1）當k=1時，y= x²＋3x+1;當k=0時y="x+1," 圖象略
(2) 對任意實數k, 函數的圖象都經過點（-2，-1）和點（0,1）
證明；把x=-2代入函數y＝kx²＋(2k＋1)x＋1，得y=-1，即函數y＝kx²＋(2k＋1)x＋1的圖像經過點（-2，-1）；把x=0代入函數y＝kx²＋(2k＋1)x＋1，得y=1，即函數y＝kx²＋(2k＋1)x＋1的圖像經過點（0,1）
（3）當k為任意負實數，該函數的圖像總是開口向下的拋物線，其對稱軸為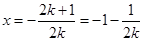，當負數k所取的值非常小時，正數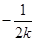靠近0，所以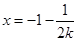靠近-1，所以只要m的值不大于-1即可。