

 •x•
•x• x=
x= x2,(0<x≤8);(2) 當x=
x2,(0<x≤8);(2) 當x= 時,y有最大值,最大值為8.
時,y有最大值,最大值為8. •x•
•x• x=
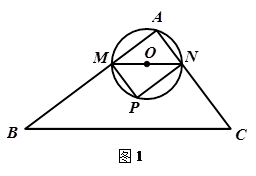
x= x2,根據二次函數的性質得到x=4,y的最大值為6;當4<x≤8時,PM與PN分別交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性質可表示出PN=AM=x;再由平行四邊形BFNM的性質解得FN=8-x,PF=2x-8,則可利用相似三角形Rt△PEF∽Rt△ABC的性質求得S△PEF值;然后寫出y與x的解析式,再根據二次函數的性質求出y的最大值,最后綜合兩種情況即可.
x2,根據二次函數的性質得到x=4,y的最大值為6;當4<x≤8時,PM與PN分別交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性質可表示出PN=AM=x;再由平行四邊形BFNM的性質解得FN=8-x,PF=2x-8,則可利用相似三角形Rt△PEF∽Rt△ABC的性質求得S△PEF值;然后寫出y與x的解析式,再根據二次函數的性質求出y的最大值,最后綜合兩種情況即可. ,
, ,解得AN=
,解得AN= x,
x, •x•
•x• x=
x= x2,
x2, •x•
•x• x=
x= x2,(0<x≤8);
x2,(0<x≤8); •x•
•x• x=
x= x2,此時x=4,y的最大值為6;
x2,此時x=4,y的最大值為6; ,
, ×8×6=24,
×8×6=24, (x-4)2,
(x-4)2, x2-
x2- (x-4)2
(x-4)2 x2+12x-24,
x2+12x-24, (x-
(x- )2+8(4<x≤8),
)2+8(4<x≤8), <0,
<0, 時,y有最大值,最大值為8,
時,y有最大值,最大值為8, 時,y有最大值,最大值為8.
時,y有最大值,最大值為8.

科目:初中數學 來源:不詳 題型:解答題
 ).則每戶平均集資的資金在150元的基礎上減少了
).則每戶平均集資的資金在150元的基礎上減少了 %,求a的值.
%,求a的值.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
 的圖象在第一象限的一支曲線上有一點A(a,c),點B(b,c+1)在該函數圖象的另外一支上,則關于一元二次方程ax2+bx+c = 0的兩根x1,x2判斷正確的是( )
的圖象在第一象限的一支曲線上有一點A(a,c),點B(b,c+1)在該函數圖象的另外一支上,則關于一元二次方程ax2+bx+c = 0的兩根x1,x2判斷正確的是( )| A.x1 + x2 >1,x1·x2 > 0 |
| B.x1 + x2 < 0,x1·x2 > 0 |
| C.0 < x1 + x2 < 1,x1·x2 > 0 |
| D.x1 + x2與x1·x2 的符號都不確定 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.沒有實數根 | B.有兩個相等的實數根 |
| C.有兩個不相等的實數根 | D.無法判斷 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com