【題目】如圖，平行四邊形ABCD中，E是BC邊上的一點，且AB=AE，若AE平分∠DAB，∠EAC=20°，則∠AED的度數為（ ）
A. 70°B. 75°C. 80°D. 85°
【答案】C
【解析】
先證明∠B=∠EAD，然后利用SAS證明△ABC≌△EAD，得出∠AED=∠BAC．再證明△ABE為等邊三角形，可得∠BAE=60°，求出∠BAC的度數，即可得∠AED的度數．
∵在平行四邊形ABCD中，AD∥BC，BC=AD，
∴∠EAD=∠AEB，
又∵AB=AE，
∴∠B=∠AEB，
∴∠B=∠EAD，
在△ABC和△EAD中，
，
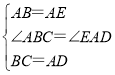∴△ABC≌△EAD（SAS），
∴∠AED=∠BAC．
∵AE平分∠DAB，
∴∠BAE=∠DAE，
∴∠BAE=∠AEB=∠B，
∴△ABE為等邊三角形，
∴∠BAE=60°，
∴∠BAC=∠BAE+∠EAC=80°，
∴∠AED=∠BAC=80°；
故選C．
科目：初中數學 來源： 題型：
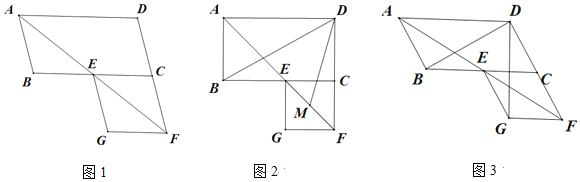
【題目】在平行四邊形ABCD中，∠BAD的平分線交線段BC于點E，交線段DC的延長線于點F，以EC、CF為鄰邊作平行四邊形ECFG．
（1）如圖1，證明平行四邊形ECFG為菱形；
（2）如圖2，若∠ABC=90°，M是EF的中點，求∠BDM的度數；
（3）如圖3，若∠ABC=120°，請直接寫出∠BDG的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
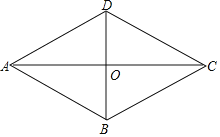
【題目】如圖，在四邊形ABCD中，AD∥BC，CA平分∠DCB，DB平分∠ADC
（1）求證：四邊形ABCD是菱形；
（2）若AC＝8，BD＝6，求點D到AB的距離
查看答案和解析>>
科目：初中數學 來源： 題型：
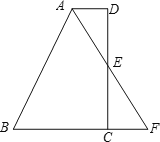
【題目】如圖，在四邊形ABCD中，AD//BC，E為CD的中點，連接AE、BE，延長AE交BC的延長線于點F.
（1）DAE 和CFE全等嗎？說明理由；
（2）若AB BCAD，說明 BE AF；
（3）在（2）的條件下，若CE 5，D 90 ，求出E到AB的距離.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學復習課上，老師出示5張背面完全相同的卡片，卡片正面分別寫有下列方程：
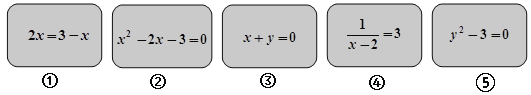
（1）若把這5張卡片的背面朝上且攪勻，從中隨機抽取一張卡片，則抽到卡片上有一元二次方程的概率是多少？
（2）請按一定的規則把這5個方程分成兩類，寫出你的分類規則，并把分類結果分別填在下列兩個大括號內（只需填方程的序號）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了了解學生參加體育活動的情況，對學生進行隨機抽樣調查，其中一個問題是“你平均每天參加體育活動的時間是多少？”共有4個選項：
A.
小時以上
小時
小時
小時以下
圖1、2是根據調查結果繪制的兩幅不完整的統計圖，請你根據統計圖提供的信息，在圖1中將選項C的部分補充完整．
本次一共調查了多少名學生？
在圖1中將選項B的部分補充完整；
若該校有3000名學生，請你估計全校可能有多少名學生平均每天參加體育活動的時間在
以下？
對此次的調查結果，請你談一點自己的看法．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在三角形
中，
.
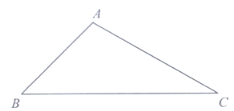
（1）按下列要求畫出相應的圖形
①過點
畫直線
;
②過點
分別畫直線
和直線
的垂線，垂足分別為點
、
，
交于點
.
（2）在（1）所畫出的圖形中，按要求完成下列問題.
①線段____________的長度是點到的距離，線段
的長度是點_______到直線__________的距離;
②在線段
、
、、
中，長度最短的是線段___________，理由是：直線外一點與直線上各點連接的所有線段中，________________最短；
③延長
至點
，試說明
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有這樣一個問題：探究函數y=
的圖象與性質。小慧根據學習函數的經驗，對函數y=
的圖象與性質進行了探究。下面是小慧的探究過程，請補充完成：
（1）函數y=
的自變量x的取值范圍是__________；
（2）列出y與x的幾組對應值。請直接寫出m的值，m=________；
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
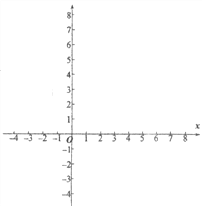
（3）請在平面直角坐標系xOy中，描出以上表中各對對應值為坐標的點，并畫出該函數的圖象；
（4）結合函數的圖象，寫出該函數的兩條性質：
①_____________________________________________；
②____________________________________________。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
