解:(1)∵兩條拋物線都經過點C(6,0),
∴-

×6
2+6b+4=0,
解得b=

,

×6
2-2×6+c=0,
解得c=6;
(2)根據題意,點A的坐標為(0,4),點B的坐標為(0,6),
所以,AB=2,
∵點P的橫坐標為m,
∴P(m,-

m
2+

m+4),
∵PQ∥y軸,
∴點Q(m,

m
2-2m+6),
∴PQ=(-

m
2+

m+4)-(

m
2-2m+6)=-

m
2+

m+4-

m
2+2m+6=-

m
2+

m-2,
∴當PQ=AB時,-

m
2+

m-2=2,
整理得,3m
2-20m+24=0,
解得m
1=
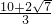
,m
2=

,
故以A、B、P、Q為頂點的四邊形是平行四邊形時,m的值為
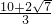
或

;
(3)由(2)知,PQ=-

m
2+

m-2=-

(m-

)
2+

,
所以,當m=

時,線段PQ的長度最大,線段PQ的最大長度為

;
(4)由(3)知,PQ=-

(m-

)
2+

,
所以,線段PQ的長度隨m增大而減小的m的取值范圍是

≤m<6.
分析:(1)把點C的坐標代入兩拋物線解析式,計算即可求出b、c的值;
(2)求出A、B的坐標,然后求出AB的長度,再根據點P的橫坐標利用拋物線解析式表示出點P、Q的坐標,然后表示出PQ的長度,根據平行四邊形的對邊平行且相等列出方程,然后求解即可得到m的值;
(3)根據線段PQ的表達式轉化為頂點式解析式,再利用二次函數的最值問題解答即可;
(4)根據PQ的表達式的頂點式形式,利用二次函數的增減性解答即可.
點評:本題考查了二次函數的綜合題型,主要利用了待定系數法求二次函數解析式,平行四邊形的對邊平行且相等的性質,二次函數的最值問題,二次函數的增減性,綜合性較強,但難度不大,把點C的坐標代入函數解析式求出b、c的值是解題的關鍵,也是本題的突破口.

 x2+bx+4、y=
x2+bx+4、y= x2-2x+c與y軸交點,兩條拋物線都經過點C(6,
x2-2x+c與y軸交點,兩條拋物線都經過點C(6,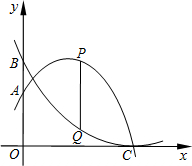 0).點P、Q分別在拋物線y=
0).點P、Q分別在拋物線y= x2+bx+4、y=
x2+bx+4、y= x2-2x+c上,點P在點Q的上方,PQ平行y軸.設點P的橫坐標為m.
x2-2x+c上,點P在點Q的上方,PQ平行y軸.設點P的橫坐標為m. ×62+6b+4=0,
×62+6b+4=0, ,
, ×62-2×6+c=0,
×62-2×6+c=0, m2+
m2+ m+4),
m+4), m2-2m+6),
m2-2m+6), m2+
m2+ m+4)-(
m+4)-( m2-2m+6)=-
m2-2m+6)=- m2+
m2+ m+4-
m+4- m2+2m+6=-
m2+2m+6=- m2+
m2+ m-2,
m-2, m2+
m2+ m-2=2,
m-2=2,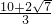 ,m2=
,m2= ,
,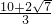 或
或 ;
; m2+
m2+ m-2=-
m-2=- (m-
(m- )2+
)2+ ,
, 時,線段PQ的長度最大,線段PQ的最大長度為
時,線段PQ的長度最大,線段PQ的最大長度為 ;
; (m-
(m- )2+
)2+ ,
, ≤m<6.
≤m<6.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 如圖,點D,E分別為AB、AC上的兩點且DE與BC不平行,請你添加任意一個條件,使△ABC與△ADE相似,添加的條件為
如圖,點D,E分別為AB、AC上的兩點且DE與BC不平行,請你添加任意一個條件,使△ABC與△ADE相似,添加的條件為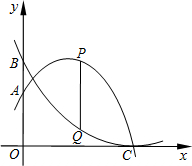 0).點P、Q分別在拋物線y=-
0).點P、Q分別在拋物線y=-