
【題目】以四邊形ABCD的邊AB,AD為邊分別向外側作等邊△ABF和等邊△ADE,連接EB,FD,交點為G.
(1)當四邊形ABCD為正方形時(如圖1),EB和FD的數量關系是 ;
(2)當四邊形ABCD為矩形時(如圖2),EB和FD具有怎樣的數量關系?請加以證明;
(3)四邊形ABCD由正方形到矩形到一般平行四邊形的變化過程中,∠EGD是否發生變化?如果改變,請說明理由.
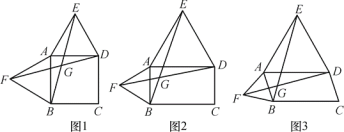
【答案】(1)EB=FD;(2)EB=FD,證明見解析;(3)∠EGD不發生變化.
【解析】
(1)利用正方形的性質、等邊三角形的性質和全等三角形的證明方法可證明△FAD≌△BAE,由全等三角形的性質即可得到EB= FD;
(2)利用長方形的性質、等邊三角形的性質和全等三角形的證明方法可證明△FAD≌△BAE,由全等三角形的性質即可得到EB= FD;
(3)四邊形ABCD由正方形到矩形到一般平行四邊形的變化過程中,∠EGD不會發生變化,是一個定值,為60°.
解:(1)EB=FD,
理由如下:

∵四邊形ABCD為正方形,
∴AB=AD,
∵以四邊形ABCD的邊AB、AD為邊分別向外側作等邊三角形ABF和ADE,
∴AF=AE,∠FAB=∠EAD=60°,
∵∠FAD=∠BAD+∠FAB=90°+60°=150°,
∠BAE=∠BAD+∠EAD=90°+60°=150°,
∴∠FAD=∠BAE,
在△AFD和△ABE中,
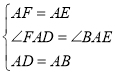 ,
,
∴△AFD≌△ABE,
∴EB=FD;
(2)EB=FD.
證:∵△AFB為等邊三角形
∴AF=AB,∠FAB=60°
∵△ADE為等邊三角形,
∴AD=AE,∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE
∴△FAD≌△BAE
∴EB=FD;
(3)解:不會發生改變;

同(2)易證:△FAD≌△BAE,
∴∠AEB=∠ADF,
設∠AEB為x°,則∠ADF也為x°
于是有∠BED為(60﹣x)°,∠EDF為(60+x)°,
∴∠EGD=180°﹣∠BED﹣∠EDF
=180°﹣(60﹣x)°﹣(60+x)°
=60°.


科目:初中數學 來源: 題型:
【題目】如圖,點O(0,0),A(0,1)是正方形OAA1B的兩個頂點,以OA1對角線為邊作正方形OA1A2B1,再以正方形的對角線OA2作正方形OA1A2B1,…,依此規律,則點A2017的坐標是( )
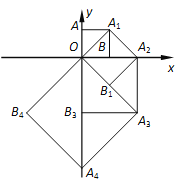
A. (0,21008) B. (21008,21008) C. (21009,0) D. (21009,-21009)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
通過整式運算一章的學習,我們發現要驗證一個結論的正確性可以有兩種方法:
例如:要驗證結論![]()
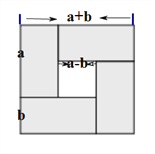
方法1:幾何圖形驗證:如下圖,我們可以將一個邊長為(a+b)的正方形上裁去一個邊長為(a-b)的小正方形則剩余圖形的面積為4ab,驗證該結論正確。
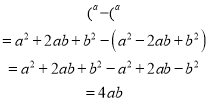
方法2:代數法驗證:等式左邊=![]() ,
,
所以,左邊=右邊,結論成立。
觀察下列各式:
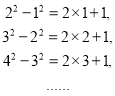
(1)按規律,請寫出第n個等式________________;
(2)試分別用兩種方法驗證這個結論的正確性.
查看答案和解析>>
科目:初中數學 來源: 題型:
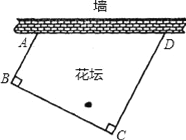
【題目】小區要用籬笆圍成一個四邊形花壇、花壇的一邊利用足夠長的墻,另三邊所用的籬笆之和恰好為18米.圍成的花壇是如圖所示的四邊形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.設AB邊的長為x米.四邊形ABCD面積為S平方米.
(1)請直接寫出S與x之間的函數關系式(不要求寫出自變量x的取值范圍).
(2)當x是多少時,四邊形ABCD面積S最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2-2![]() x+m=0有兩個不相等的實數根.
x+m=0有兩個不相等的實數根.
(1)求實數m的最大整數值;
(2)在(1)的條件下,方程的實數根是x1,x2,求代數式![]() +
+![]() -
-![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
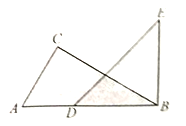
【題目】如圖,一副三角板的三個內角分別是![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,按如圖所示疊放在一起(點
,按如圖所示疊放在一起(點![]() 在同一直線上),若固定
在同一直線上),若固定![]() ,將
,將![]() 繞著公共頂點
繞著公共頂點![]() 順時針旋轉
順時針旋轉![]() 度(
度(![]() ),當邊
),當邊![]() 與
與![]() 的某一邊平行時,相應的旋轉角
的某一邊平行時,相應的旋轉角![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
對于多項式![]() ,如果我們把
,如果我們把![]() 代入此多項式,發現
代入此多項式,發現![]() 的值為0,這時可以確定多項式中有因式
的值為0,這時可以確定多項式中有因式![]() :同理,可以確定多項式中有另一個因式
:同理,可以確定多項式中有另一個因式![]() ,于是我們可以得到:
,于是我們可以得到:![]() .
.
又如:對于多項式![]() ,發現當
,發現當![]() 時,
時,![]() 的值為0,則多項式
的值為0,則多項式![]() 有一個因式
有一個因式![]() ,我們可以設
,我們可以設![]() ,解得
,解得![]() ,
,![]() ,于是我們可以得到:
,于是我們可以得到:![]() .
.
請你根據以上材料,解答以下問題:
(1)當![]() 時,多項式
時,多項式![]() 的值為0,所以多項式
的值為0,所以多項式![]() 有因式 ,從而因式分解
有因式 ,從而因式分解![]() .
.
(2)以上這種因式分解的方法叫試根法,常用來分解一些比較復雜的多項式.請你嘗試用試根法分解多項式:①![]() ;②
;②![]() .
.
(3)小聰用試根法成功解決了以上多項式的因式分解,于是他猜想:
代數式![]() 有因式 , , ,
有因式 , , ,
所以分解因式![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形OABC中,O為平面直角坐標系的原點,A點的坐標為(4,0),C點的坐標為(0,6),點B在第一象限內,點P從原點O出發,以每秒2個單位長度的速度沿著O﹣A﹣B﹣C﹣O的路線移動(即沿長方形移動一周).
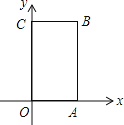
(1)寫出B點的坐標;
(2)當點P移動3秒時,求三角形OAP的面積;
(3)在移動過程中,當點P到x軸距離為4個單位長度時,求點P移動的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的中線BD,CE交于點O,F,G分別是BO,CO的中點.
(1)求證:四邊形DEFG是平行四邊形.
(2)若AB=AC,則四邊形DEFG是 (填寫特殊的平行四邊形).
(3)若四邊形DEFG是邊長為2的正方形,試求△ABC的周長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com