
請嘗試解決以下問題:
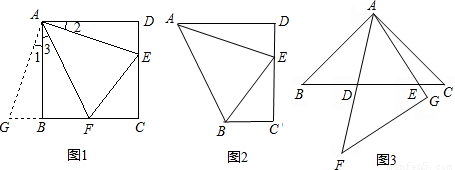
(1)如圖1,在正方形ABCD中,點E,F分別為DC,BC邊上的點,且滿足∠EAF=45°,連接EF,求證DE+BF=EF.
感悟解題方法,并完成下列填空:
將△ADE繞點A順時針旋轉90°得到△ABG,此時AB與AD重合,

由旋轉可得:AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,點G,B,F在同一條直線上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)運用(1)解答中所積累的經驗和知識,完成下題:
如圖2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一點,且∠BAE=45°,DE=4,求BE的長.

(2)類比(1)證明思想完成下列問題:在同一平面內,將兩個全等的等腰直角三角形ABC和AFG擺放在一起,A為公共頂點,∠BAC=∠AGF=90°,若∆ABC固定不動,∆AFG繞點A旋轉,AF、AG與邊BC的交點分別為D、E(點D不與點B重合,點E不與點C重合),在旋轉過程中,等式BD +CE
+CE =DE
=DE 始終成立,請說明理由.
始終成立,請說明理由.
解:(1)EAF、△EAF、GF
(2) 過A作AG⊥BC,交BC延長線于G.

在直角梯形ABCD中,
∵AD∥BC,∴∠C=∠D=90°,
又∠CGA=90°,AD=CD,
∴四邊形AGCD 為正方形.
∴CG=AD=10.
已知∠BAE=45°,
根據(1)可知,BE=GB+DE.
設BE=x,則BG=x-4,
∴BC=14-x.
在Rt△BCE中, ∵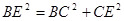 ,即
,即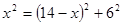 .
.
解這個方程,得:x=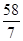 .
.
∴BE=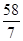 .
.
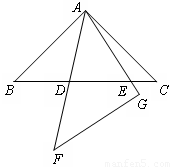
(3)證明:如下圖,將∆ACE繞點A順時針旋轉90°至∆ABH的位置,
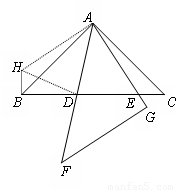
則CE=HB,AE=AH,∠ABH=∠C=45°,旋轉角∠EAH=90°.
連接HD,在∆EAD和∆HAD中
∵AE=AH,∠HAD=∠EAH-∠FAG=45°=∠EAD, AD=AD.
∴∆EAD≌∆HAD ∴DH=DE
又∠HBD=∠ABH+∠ABD=90° ∴BD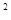 +HB
+HB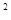 =DH
=DH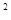
即BD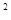 +CE
+CE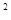 =DE
=DE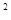
【解析】(1)利用角之間的等量代換得出∠GAF=∠FAE,再利用SAS得出△GAF≌△EAF,得出答案;
(2)過A作AG⊥BC,交BC延長線于G,由正方形的性質得出CG=AD=10,再運用勾股定理和方程求出BE的長;
(3)運用旋轉性質和勾股定理判斷說明等式成立.


科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2012屆廣東省佛山市南海區九年級上學期期末考試數學試卷(帶解析) 題型:解答題
請嘗試解決以下問題:
(1)如圖1,在正方形ABCD中,點E,F分別為DC,BC邊上的點,且滿足∠EAF=45°,連接EF,求證DE+BF=EF.
感悟解題方法,并完成下列填空:
將△ADE繞點A順時針旋轉90°得到△ABG,此時AB與AD重合,
由旋轉可得:AB="AD,BG=DE," ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,點G,B,F在同一條直線上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)運用(1)解答中所積累的經驗和知識,完成下題:
如圖2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一點,且∠BAE=45°,DE=4,求BE的長.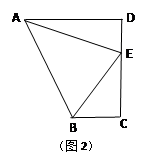
(3)類比(1)證明思想完成下列問題:在同一平面內,將兩個全等的等腰直角三角形ABC和AFG擺放在一起,A為公共頂點,∠BAC=∠AGF=90°,若∆ABC固定不動,∆AFG繞點A旋轉,AF、AG與邊BC的交點分別為D、E(點D不與點B重合,點E不與點C重合),在旋轉過程中,等式BD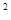 +CE
+CE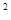 =DE
=DE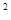 始終成立,請說明理由.
始終成立,請說明理由.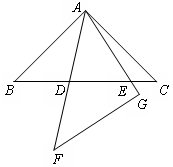
查看答案和解析>>
科目:初中數學 來源:2011-2012學年廣東省佛山市南海區九年級(上)期末數學試卷(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2012年云南省昆明十中中考數學一模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com