
【題目】重慶市有![]() 五個景區很受游客喜愛,一旅行社對某小區居民在暑假期間去以上五個景區旅游(只選一個景區)的意向做了一次隨機調查統計,并根據這個統計結果制作了如下兩幅不完整的統計圖.
五個景區很受游客喜愛,一旅行社對某小區居民在暑假期間去以上五個景區旅游(只選一個景區)的意向做了一次隨機調查統計,并根據這個統計結果制作了如下兩幅不完整的統計圖.

![]() 該小區居民在這次隨機調查中被調查到的人數是_______人,
該小區居民在這次隨機調查中被調查到的人數是_______人, ![]() 想去
想去![]() 景區的人有_________人, 并補全條形統計圖.
景區的人有_________人, 并補全條形統計圖.
![]() 被調查到的居民想去 景區旅游的人數最多,若該小區有居民
被調查到的居民想去 景區旅游的人數最多,若該小區有居民![]() 人,估計去該景區旅游的居民約有多少人?
人,估計去該景區旅游的居民約有多少人?
![]() 小強同學贊假期間計劃與父母從
小強同學贊假期間計劃與父母從![]() 五個景區中,任選兩個去旅游,求選至
五個景區中,任選兩個去旅游,求選至![]() 兩個景區的概率,(要求列表求概率)
兩個景區的概率,(要求列表求概率)
【答案】(1)200,35%,40,補全條形統計圖見解析;(2)B,700;(3)![]()
【解析】
(1)用想去D景區的人數除以它所占的百分比得到調查的總人數,再計算想去B景區的百分比得到m的值,然后計算出想去C景區的人數后補全條形統計圖;
(2)利用條形條形圖可判斷想去B景區旅游的人數最多,用2000乘以m%可估計該景區旅游的居民大約人數;
(3)畫樹狀圖展示所有12種等可能的結果數,找出選到B,D兩個景區的結果數,然后根據概率公式計算.
解:(1)20÷10%=200,
所以該小區居民在這次隨機調查中被調查到的人數是200人,
m%=![]() ×100%=35%,即m=35;
×100%=35%,即m=35;
想去C景區的人數為:200﹣20﹣70﹣20﹣50=40(人),
故答案為200,35%,40.
補全條形統計圖為:

(2)被調查到的居民想去B景區旅游的人數最多,
故答案為:B.
2000×35%=700,
所以估計去該景區旅游的居民約有700人;
(3)列表如下:
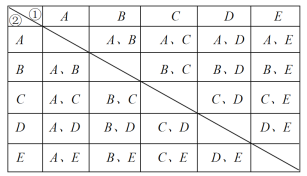
共有20種等可能的結果數,其中選到B,D兩個景區的結果數為2,
所以選到B,D兩個景區的概率=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系內,點![]() 為坐標原點,
為坐標原點,![]() 的頂點
的頂點![]() 在
在![]() 軸正半軸,頂點
軸正半軸,頂點![]() 、
、![]() 分別在
分別在![]() 軸負半軸和正半軸上,
軸負半軸和正半軸上,![]() ,
,![]() ,
,![]()
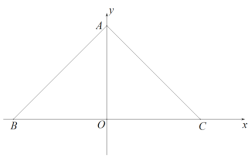
(1)求![]() 的長.
的長.
(2)動點![]() 從點
從點![]() 出發以每秒
出發以每秒![]() 個單位長度的速度沿
個單位長度的速度沿![]() 向終點
向終點![]() 運動,點
運動,點![]() 運動的時間為
運動的時間為![]() ,以
,以![]() 為斜邊在
為斜邊在![]() 右邊上方作等腰直角三角形
右邊上方作等腰直角三角形![]() ,連接
,連接![]() 、
、![]() ,設
,設![]() 的面積為
的面積為![]() (
(![]() ),求
),求![]() 與
與![]() 之間的函數關系式,并直接寫出自變量
之間的函數關系式,并直接寫出自變量![]() 的取值范圍.
的取值范圍.
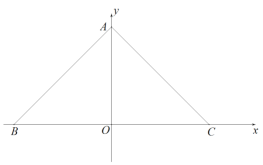
(3)在(2)的條件下,過點![]() 作
作![]() 的垂線交
的垂線交![]() 軸于
軸于![]() ,連接
,連接![]() ,當四邊形
,當四邊形![]() 的面積為
的面積為![]() ,時,求
,時,求![]() 的值及
的值及![]() 點坐標.
點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在長方形ABCD內,將兩張邊長分別為a和b(a>b)的正方形紙片按圖1,圖2兩種方式放置(圖1,圖2中兩張正方形紙片均有部分重疊),設圖1中未被這兩張正方形紙片覆蓋的面積為S1,圖2中未被這兩張正方形紙片覆蓋的面積為S2,當S2-S1=b時,AD-AB的值為( )

A.1B.2C.2a-2bD.b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線MN與直線AB、CD分別交于點E、F,∠1與∠2互補.
(1)試判斷直線AB與直線CD的位置關系,并說明理由;
(2)如圖2,∠BEF與∠EFD的角平分線交于點P,EP與CD交于點G,點H是MN上一點,且GH⊥EG,求證:PF∥GH;
(3)如圖3,在(2)的條件下,連接PH,K是GH上一點使∠PHK=∠HPK,作PQ平分∠EPK,問∠HPQ的大小是否發生變化?若不變,請求出其值;若變化,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,![]() ,
,![]() ,且
,且![]() .
.
(1)求點A、B的坐標;
(2)如圖1,P點為y軸正半軸上一點,連接BP,若![]() ,請求出P點的坐標;
,請求出P點的坐標;
(3)如圖2,已知![]() ,若C點是x軸上一個動點,是否存在點C,使
,若C點是x軸上一個動點,是否存在點C,使![]() ,若存在,請直接寫出所有符合條件的點C的坐標;若不存在,請說明理由.
,若存在,請直接寫出所有符合條件的點C的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在⊙O中,直徑AB=6,BC是弦,∠ABC=30°,點P在BC上,點Q在⊙O上,且OP⊥PQ.
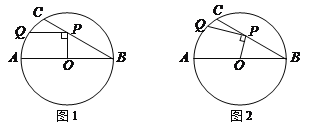
(1)如圖1,當PQ∥AB時,求PQ的長度;
(2)如圖2,當點P在BC上移動時,求PQ長的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
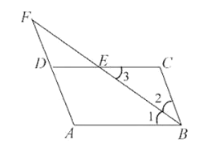
【題目】如圖,在四邊形![]() 中,
中,![]() 的平分線交
的平分線交![]() 于點
于點![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,
,![]()
(1)寫出![]() 對由條件
對由條件![]() 推出的相等或互補的角
推出的相等或互補的角
(2)![]() 與
與![]() 相等嗎?為什么?
相等嗎?為什么?
(3)證明:![]()
請在下面的括號內,填上推理的根據,并完成下面的證明:
![]() ( ① )
( ① )
![]() (已證),
(已證),![]() ,( ② )
,( ② )
又![]() (角平分線的定義)
(角平分線的定義)
![]() ( ③ )
( ③ )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com