
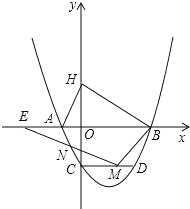
【題目】如圖,已知拋物線與x軸交于A(﹣1,0),B(4,0),與y軸交于C(0,﹣2).
(1)求拋物線的解析式;
(2)H是C關于x軸的對稱點,P是拋物線上的一點,當△PBH與△AOC相似時,求符合條件的P點的坐標(求出兩點即可);
(3)過點C作CD∥AB,CD交拋物線于點D,點M是線段CD上的一動點,作直線MN與線段AC交于點N,與x軸交于點E,且∠BME=∠BDC,當CN的值最大時,求點E的坐標.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)P的坐標為(﹣1,0)或(8,18);(3)E的坐標為(﹣
x﹣2;(2)P的坐標為(﹣1,0)或(8,18);(3)E的坐標為(﹣![]() ,0).
,0).
【解析】
試題分析:(1)由拋物線與x軸交于A(﹣1,0),B(4,0),可設拋物線的解析式為y=a(x+1)(x﹣4),然后將(0,﹣2)代入解析式即可求出a的值;(2)當△PBH與△AOC相似時,△PBH是直角三角形,由![]() 可知∠AHB=90°,根據待定系數法求出直線AH的解析式后,聯立一次函數與二次函數的解析式后即可求出P的坐標;(3)設M的坐標為(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用對應邊的比相等即可得出CN與m的函數關系式,利用二次函數的性質即可求出m=
可知∠AHB=90°,根據待定系數法求出直線AH的解析式后,聯立一次函數與二次函數的解析式后即可求出P的坐標;(3)設M的坐標為(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用對應邊的比相等即可得出CN與m的函數關系式,利用二次函數的性質即可求出m=![]() 時,CN有最大值,然后再證明△EMB∽△BDM,即可求出E的坐標.
時,CN有最大值,然后再證明△EMB∽△BDM,即可求出E的坐標.
試題解析:(1)∵拋物線與x軸交于A(﹣1,0),B(4,0),
∴設拋物線的解析式為:y=a(x+1)(x﹣4),
把(0,﹣2)代入y=a(x+1)(x﹣4),
∴a=![]() ,
,
∴拋物線的解析式為:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)當△PBH與△AOC相似時,
∴△AOC是直角三角形,
∴△PBH也是直角三角形,
由題意知:H(0,2),
∴OH=2,
∵A(﹣1,0),B(4,0),
∴OA=1,OB=4,
∴![]()
∵∠AOH=∠BOH,
∴△AOH∽△BOH,
∴∠AHO=∠HBO,
∴∠AHO+∠BHO=∠HBO+∠BHO=90°,
∴∠AHB=90°,
設直線AH的解析式為:y=kx+b,
把A(﹣1,0)和H(0,2)代入y=kx+b,
∴![]() ,
,
∴解得k=2,b=2,
∴直線AH的解析式為:y=2x+2,
聯立 ,
,
解得:x=1或x=﹣8,
當x=﹣1時,
y=0,
當x=8時,
y=18
∴P的坐標為(﹣1,0)或(8,18)
(3)過點M作MF⊥x軸于點F,
設點E的坐標為(n,0),M的坐標為(m,0),
∵∠BME=∠BDC,
∴∠EMC+∠BME=∠BDC+∠MBD,
∴∠EMC=∠MBD,
∵CD∥x軸,
∴D的縱坐標為﹣2,
令y=﹣2代入y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
∴x=0或x=3,
∴D(3,﹣2),
∵B(4,0),
∴由勾股定理可求得:BD=![]() ,
,
∵M(m,0),
∴MD=3﹣m,CM=m(0≤m≤3)
∴由拋物線的對稱性可知:∠NCM=∠BDC,
∴△NCM∽△MDB,
∴![]() ,
,
∴![]() ,
,
∴CN=![]() ,
,
∴當m=![]() 時,CN可取得最大值,
時,CN可取得最大值,
∴此時M的坐標為(![]() ,﹣2),
,﹣2),
∴MF=2,BF=![]() ,MD=
,MD=![]()
∴由勾股定理可求得:MB=![]() ,
,
∵E(n,0),
∴EB=4﹣n,
∵CD∥x軸,
∴∠NMC=∠BEM,∠EBM=∠BMD,
∴△EMB∽△BDM,
∴![]() ,
,
∴MB2=MDEB,
∴![]() =
=![]() ×(4﹣n),
×(4﹣n),
∴n=﹣![]() ,
,
∴E的坐標為(﹣![]() ,0).
,0).


科目:初中數學 來源: 題型:
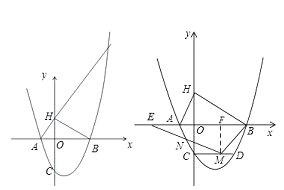
【題目】二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,圖象過點(﹣1,0),對稱軸為直線x=2,下列結論:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若點A(﹣3,y1)、點B(﹣![]() ,y2)、點C(
,y2)、點C(![]() ,y3)在該函數圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結論有( )
,y3)在該函數圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結論有( )
A.2個 B.3個 C.4個 D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
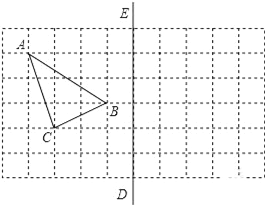
【題目】如圖,在所給正方形網格圖中完成下列各題:(用直尺畫圖,保留痕跡)
(1)畫出格點△ABC(頂點均在格點上)關于直線DE對稱的△A1B1C1;
(2)在DE上畫出點Q,使QA+QC最小.
查看答案和解析>>
科目:初中數學 來源: 題型:
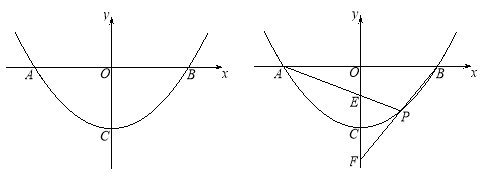
【題目】拋物線y=ax2+c與x軸交于A、B兩點,頂點為C,點P為拋物線上,且位于x軸下方.
(1)如圖1,若P(1,-3)、B(4,0),
① 求該拋物線的解析式;
② 若D是拋物線上一點,滿足∠DPO=∠POB,求點D的坐標;
(2) 如圖2,已知直線PA、PB與y軸分別交于E、F兩點.當點P運動時,![]() 是否為定值?若是,試求出該定值;若不是,請說明理由.
是否為定值?若是,試求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】巴黎與北京的時間差為﹣7時(正數表示同一時刻比北京時間早的時數),如果北京時間是7月2日14:00,那么巴黎時間是( )
A. 7月2日21時 B. 7月2日7時 C. 7月1日7時 D. 7月2日5時
查看答案和解析>>
科目:初中數學 來源: 題型:
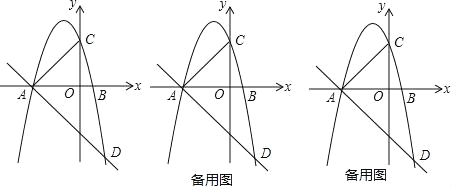
【題目】已知拋物線y=a(x+3)(x﹣1)(a≠0),與x軸從左至右依次相交于A、B兩點,與y軸相交于點C,經過點A的直線y=﹣![]() x+b與拋物線的另一個交點為D.
x+b與拋物線的另一個交點為D.
(1)若點D的橫坐標為2,求拋物線的函數解析式;
(2)若在第三象限內的拋物線上有點P,使得以A、B、P為頂點的三角形與△ABC相似,求點P的坐標;
(3)在(1)的條件下,設點E是線段AD上的一點(不含端點),連接BE.一動點Q從點B出發,沿線段BE以每秒1個單位的速度運動到點E,再沿線段ED以每秒![]() 個單位的速度運動到點D后停止,問當點E的坐標是多少時,點Q在整個運動過程中所用時間最少?
個單位的速度運動到點D后停止,問當點E的坐標是多少時,點Q在整個運動過程中所用時間最少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com