【答案】
分析:(1)因?yàn)锳BCD和AEFG為正方形,所以∠GAE=∠BAD=90°,等號(hào)兩邊都加上∠EAB,得到∠GAB=∠EAD,且AG=AE,AD=AB,利用“SAS”即可得證;
(2)∠BHD=90°,理由是:由(1)得出的三角形全等,得到∠ADE與∠ABG相等,再根據(jù)對(duì)頂角相等,由兩對(duì)角相等的三角形相似得到△AND與△HNB相似,由相似三角形的對(duì)應(yīng)角相等得到∠BHD與∠BAD相等,而根據(jù)正方形ABCD得到∠BAD為90°,故∠BHD=90°;
(3)根據(jù)旋轉(zhuǎn)角∠BAE為銳角,直角及鈍角分為三種情況考慮:①當(dāng)∠BAE為銳角時(shí),如圖所示,過點(diǎn)B作BM⊥直線AE于點(diǎn)M,過點(diǎn)D作DN⊥直線AG于點(diǎn)N.根據(jù)同角的余角相等得到∠MAB=∠NAD,由正方形的性質(zhì)得到AB=AD,再由垂直得到一對(duì)直角相等,利用“AAS”得到△AND≌△AMB,根據(jù)全等三角形的對(duì)應(yīng)邊相等得到DN=BM,又AE=AG,根據(jù)等底等高的兩三角形面積相等得S
1與S
2相等;②當(dāng)∠BAE為直角時(shí),如圖所示,利用“SAS”得到△AGD與△ABE全等,故面積相等;③當(dāng)∠BAE為鈍角時(shí),如圖所示,根據(jù)①的思路,同理得到S
1與S
2相等,綜上所述,在(3)的條件下,總有S
1=S
2.
解答:(1)證明:在正方形ABCD和正方形AEFG中,
∵∠GAE=∠BAD=90°,
∴∠GAE+∠EAB=∠BAD+∠EAB,
即∠GAB=∠EAD,
又AG=AE,AB=AD,
∴△ABG≌△ADE;
(2)猜想∠BHD=90°.理由如下:
設(shè):AB和DE交于點(diǎn)N,
∵正方形ABCD,
∴∠BAD=90°,
又∵△ABG≌△ADE,
∴∠ABG=∠ADE,又∠AND=∠BNH,
∴△AND∽△HNB,
則∠BHD=∠BAD=90°;(7分)
(3)證明:當(dāng)正方形ABCD繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)0°<∠BAE<180°時(shí),S
1和S
2總保持相等.(8分)
證明如下:由于0°<∠BAE<180°分三種情況:
①當(dāng)0°<∠BAE<90°時(shí) (如圖所示)
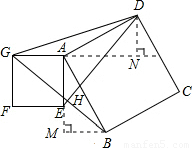
過點(diǎn)B作BM⊥直線AE于點(diǎn)M,過點(diǎn)D作DN⊥直線AG于點(diǎn)N,
∵∠MAN=∠BAD=90°,
∴∠MAB+∠BAN=90°,∠BAN+∠DAN=90°,
∴∠MAB=∠DAN,
又∠AMB=∠AND=90°,且AB=AD,
∴△AND≌△AMB,
∴BM=DN,又AE=AG,
∴

AE•BM=

AG•DN,
∴S
1=S
2;(9分)
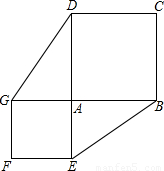
②當(dāng)∠BAE=90°時(shí),如圖所示:
∵AE=AG,∠BAE=∠DAG=90°,AB=AD,
∴△ABE≌△ADG,
∴S
1=S
2;(10分)
③當(dāng)90°<∠BAE<180°時(shí) 如圖所示:
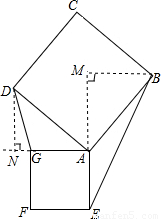
過點(diǎn)B作BM⊥直線AE于點(diǎn)M,過點(diǎn)D作DN⊥直線AG的延長(zhǎng)線于點(diǎn)N.
∵∠MAN=∠BAD=90°,
∴∠MAB+∠DAM=90°,∠DAN+∠DAM=90°,
∴∠MAB=∠NAD,
由正方形ABCD,得到∠AMB=∠AND=90°,且AB=AD,
∴△AMB≌△AND,
∴BM=DN,又AE=AG,
∴
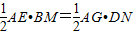
,
∴S
1=S
2,
綜上所述,在(3)的條件下,總有S
1=S
2.(11分)
點(diǎn)評(píng):此題綜合考查了正方形的性質(zhì),全等三角形的判定與性質(zhì),以及旋轉(zhuǎn)的知識(shí).學(xué)生作第三問時(shí)注意利用分類討論及數(shù)形結(jié)合的數(shù)學(xué)思想解決問題,在證明時(shí)注意運(yùn)用等底等高的兩三角形面積相等這個(gè)性質(zhì).



 AE•BM=
AE•BM= AG•DN,
AG•DN,
 過點(diǎn)B作BM⊥直線AE于點(diǎn)M,過點(diǎn)D作DN⊥直線AG的延長(zhǎng)線于點(diǎn)N.
過點(diǎn)B作BM⊥直線AE于點(diǎn)M,過點(diǎn)D作DN⊥直線AG的延長(zhǎng)線于點(diǎn)N.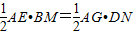 ,
,

 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案
 如圖,四邊形ABCD的對(duì)角線AC與BD互相垂直平分于點(diǎn)O,設(shè)AC=2a,BD=2b,請(qǐng)推導(dǎo)這個(gè)四邊形的性質(zhì).(至少3條)
如圖,四邊形ABCD的對(duì)角線AC與BD互相垂直平分于點(diǎn)O,設(shè)AC=2a,BD=2b,請(qǐng)推導(dǎo)這個(gè)四邊形的性質(zhì).(至少3條) 如圖,四邊形ABCD的對(duì)角線AC、BD交于點(diǎn)P,過點(diǎn)P作直線交AD于點(diǎn)E,交BC于點(diǎn)F.若PE=PF,且AP+AE=CP+CF.
如圖,四邊形ABCD的對(duì)角線AC、BD交于點(diǎn)P,過點(diǎn)P作直線交AD于點(diǎn)E,交BC于點(diǎn)F.若PE=PF,且AP+AE=CP+CF.