
【題目】已知拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,與
,與![]() 軸的一個交點坐標為
軸的一個交點坐標為![]() ,其部分圖象如圖所示,有下列結論:①
,其部分圖象如圖所示,有下列結論:①![]() ;②
;②![]() ;③當
;③當![]() 時,
時,![]() 隨
隨![]() 增大而增大;④拋物線的頂點坐標為
增大而增大;④拋物線的頂點坐標為![]() ;⑤若方程
;⑤若方程![]() 兩根為
兩根為![]() (
(![]() ),則
),則![]() ,
,![]() .其中正確結論有( )
.其中正確結論有( )

A.1個B.2個C.3個D.4個
【答案】B
【解析】
由拋物線的對稱軸結合拋物線與x軸的一個交點坐標,可求出另一交點坐標,結論①錯誤;當x=-1時,y>0,得到a-b+c>0,結論②錯誤;根據拋物線的對稱性得到結論③錯誤;將x=2代入二次函數解析式中結合4a+b+c=0,即可求出拋物線的頂點坐標,結論④正確;根據拋物線![]() 的圖象與直線
的圖象與直線![]() 的交點情況判斷⑤.
的交點情況判斷⑤.
①∵拋物線![]() a≠0)的對稱軸為直線x=2,與x軸的一個交點坐標為(4,0),
a≠0)的對稱軸為直線x=2,與x軸的一個交點坐標為(4,0),
∴拋物線與x軸的另一交點坐標為(0,0),
∴拋物線過原點,
∴![]() ,
,
∴![]() ,結論①錯誤;
,結論①錯誤;
②∵當x=-1時,y>0,
∴a-b+c>0,結論②錯誤;
③∵拋物線開口向上,
∴當x<2時,y隨x增大而減小,③錯誤;
④拋物線![]() a≠0)的對稱軸為直線x=2,且拋物線過原點,
a≠0)的對稱軸為直線x=2,且拋物線過原點,
∴![]() ,
,![]() ,
,
∴![]() ,
,
當![]() 時,
時,![]() ,
,
∴拋物線的頂點坐標為![]() ,結論④正確;
,結論④正確;
⑤∵拋物線與x軸的交點坐標為(4,0),(0,0),
∴拋物線的解析式也可以寫作:![]() ,
,
方程![]() 兩根
兩根![]() ,可以看作是:拋物線
,可以看作是:拋物線![]() 與直線
與直線![]() 的兩個交點的橫坐標,
的兩個交點的橫坐標,
∴![]() ,結論⑤正確;
,結論⑤正確;
綜上所述,正確的結論有:④⑤.
故選:B.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
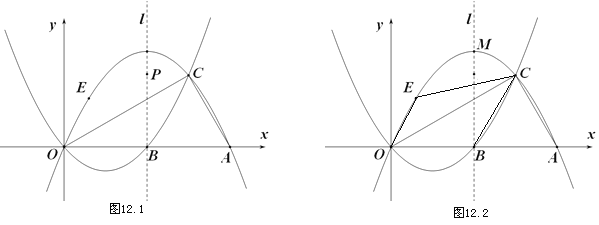
【題目】如圖,拋物線![]() :
:![]() 與
與![]() :
:![]() 相交于點
相交于點![]() 、
、![]() ,
,![]() 與
與![]() 分別交
分別交![]() 軸于點
軸于點![]() 、
、![]() ,且
,且![]() 為線段
為線段![]() 的中點.
的中點.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面積;
的面積;
(3)拋物線![]() 的對稱軸為
的對稱軸為![]() ,頂點為
,頂點為![]() ,在(2)的條件下:
,在(2)的條件下:
①點![]() 為拋物線
為拋物線![]() 對稱軸
對稱軸![]() 上一動點,當
上一動點,當![]() 的周長最小時,求點
的周長最小時,求點![]() 的坐標;
的坐標;
②如圖12.2,點![]() 在拋物線
在拋物線![]() 上點
上點![]() 與點
與點![]() 之間運動,四邊形
之間運動,四邊形![]() 的面積是否存在最大值?若存在,求出面積的最大值和點
的面積是否存在最大值?若存在,求出面積的最大值和點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l切⊙O于點A,B為⊙O上一點,過點B作BC⊥l,垂足為點C,連接AB、OB.
(1)求證:∠ABC=∠ABO;
(2)若AB=![]() ,AC=1,求⊙O的半徑.
,AC=1,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2-2(k-3)x+k2-4k-1=0.
(1)若這個方程有實數根,求k的取值范圍;
(2)若這個方程有一個根為1,求k的值;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售一種商品,經市場調查發現,該商品的周銷售量![]() (件)是售價
(件)是售價![]() (元/件)的一次函數.其售價、周銷售量、周銷售利潤
(元/件)的一次函數.其售價、周銷售量、周銷售利潤![]() (元)的三組對應值如下表:
(元)的三組對應值如下表:
售價 | 50 | 60 | 80 |
周銷售量 | 100 | 80 | 40 |
周銷售利潤 | 1000 | 1600 | 1600 |
注:周銷售利潤=周銷售量×(售價-進價)
(1)求![]() 關于
關于![]() 的函數解析式(不寫出自變量的取值范圍);
的函數解析式(不寫出自變量的取值范圍);
(2)該商品進價是 元/件;求售價是多少元/件時,周銷售利潤最大,最大利潤是多少元?
(3)由于某種原因,該商品進價提高了![]() 元/件(
元/件(![]() ),物價部門規定該商品售價不得超過65元/件.該商店在今后的銷售中,周銷售量與售價仍然滿足(1)中函數關系.若周銷售最大利潤是1400元,則
),物價部門規定該商品售價不得超過65元/件.該商店在今后的銷售中,周銷售量與售價仍然滿足(1)中函數關系.若周銷售最大利潤是1400元,則![]() 的值為 .
的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
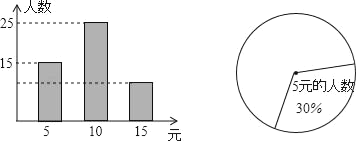
【題目】如圖是某校九年級學生為災區捐款情況抽樣調查的條形圖和扇形統計圖.
(1)求抽樣調查的人數;
(2)在扇形統計圖中,求該樣本中捐款15元的人數所占的圓心角度數;
(3)若該校九年級學生有1000人,據此樣本估計九年級捐款總數為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
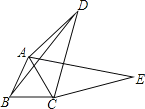
【題目】如圖,四邊形ABCD中,AC,BD是對角線,△ABC是等邊三角形.線段CD繞點C順時針旋轉60°得到線段CE,連接AE.
(1)求證:AE=BD;
(2)若∠ADC=30°,AD=3,BD=4![]() .求CD的長.
.求CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com