
【題目】如圖,五邊形![]() 內接于
內接于![]() ,
,![]() 與
與![]() 相切于點
相切于點![]() ,交
,交![]() 延長線于點
延長線于點![]() .
.
(1)若![]() ,求證:
,求證:![]() ;
;
(2)若![]() ,求
,求![]() 的長.
的長.

【答案】(1)見解析;(2)![]() .
.
【解析】
(1)由圓心角、弧、弦之間的關系得出![]() ,由圓周角定理得出∠ADE=∠DBC,證明△ADE≌△DBC,即可得出結論;
,由圓周角定理得出∠ADE=∠DBC,證明△ADE≌△DBC,即可得出結論;
(2)連接CO并延長交AB于G,作OH⊥AB于H,則∠OHG=∠OHB=90°,由切線的性質得出∠FCG=90°,得出△CFG、△OGH是等腰直角三角形,得出CF=CG,OG=![]() OH,由等邊三角形的性質得出∠OBH=30°,由直角三角形的性質得出OH=
OH,由等邊三角形的性質得出∠OBH=30°,由直角三角形的性質得出OH=![]() OB=1,OG=
OB=1,OG=![]() ,即可得出答案.
,即可得出答案.
(1)證明:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,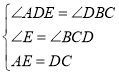 ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:連接![]() 并延長交
并延長交![]() 于
于![]() ,作
,作![]() 于
于![]() ,如圖所示:
,如圖所示:
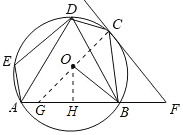
則![]() ,
,
∵![]() 與
與![]() 相切于點
相切于點![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 、
、![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數(shù)學 來源: 題型:
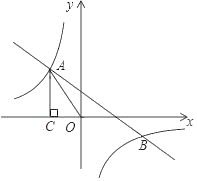
【題目】如圖,一次函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象交于第二、四象限內的點
的圖象交于第二、四象限內的點![]() 和點
和點![]() .過點
.過點![]() 作
作![]() 軸的垂線,垂足為點
軸的垂線,垂足為點![]() ,
,![]() 的面積為4.
的面積為4.
(1)分別求出![]() 和
和![]() 的值;
的值;
(2)結合圖象直接寫出![]() 的解集;
的解集;
(3)在![]() 軸上取點
軸上取點![]() ,使
,使![]() 取得最大值時,求出點
取得最大值時,求出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為2,∠A=60°,點P和點Q分別從點B和點C出發(fā),沿射線BC向右運動并且始終保持BP=CQ,過點Q作QH⊥BD,垂足為H,連接PH,設點P運動的距離為x(0<x≤2),△BPH的面積為s,則能反映s與x之間的函數(shù)關系的圖象大致為 ( )
A.  B.
B. 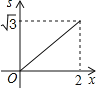 C.
C. 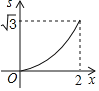 D.
D. 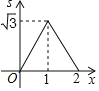
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
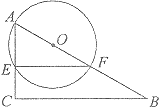
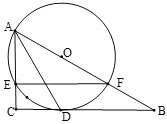
【題目】如圖,![]() 中,
中,![]() ,
,![]() 為
為![]() 上一點,
上一點,![]() 經過點
經過點![]() ,與
,與![]() 相交于點E,與
相交于點E,與![]() 交于點
交于點![]() ,連接
,連接![]() .
.
(I).如圖,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
(II)如圖,![]() 平分
平分![]() ,交
,交![]() 于點
于點![]() ,
,![]() 經過點
經過點![]() .
.
①求證:![]() 為
為![]() 的切線;
的切線;
②若![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
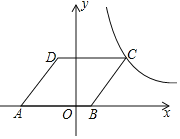
【題目】如圖,在平面直角坐標系中,點O為坐標原點,菱形ABCD的頂點B在x軸的正半軸上,點A坐標為(-4,0),點D的坐標為(-1,4),反比例函數(shù)![]() 的圖象恰好經過點C,則k的值為______.
的圖象恰好經過點C,則k的值為______.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖是王阿姨晚飯后步行的路程s(單位:m)與時間t(單位:min)的函數(shù)圖象,其中曲線段AB是以B為頂點的拋物線一部分.下列說法不正確的是( )
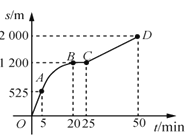
A.25min~50min,王阿姨步行的路程為800m
B.線段CD的函數(shù)解析式為![]()
C.5min~20min,王阿姨步行速度由慢到快
D.曲線段AB的函數(shù)解析式為![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】要在一塊長52m,寬48m的矩形綠地上,修建同樣寬的兩條互相垂直的甬路.下面分別是小亮和小穎的設計方案.
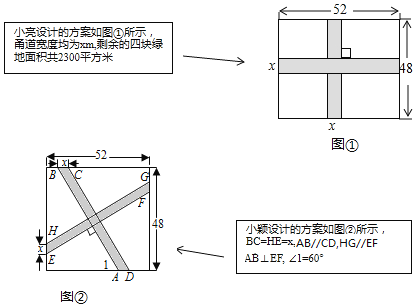
(1)求小亮設計方案中甬路的寬度x;
(2)求小穎設計方案中四塊綠地的總面積(友情提示:小穎設計方案中的與小亮設計方案中的取值相同)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
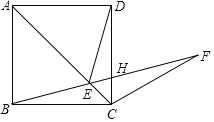
【題目】如圖,在正方形ABCD的對角線AC上取一點E.使得![]() ,連接BE并延長BE到F,使
,連接BE并延長BE到F,使![]() ,BF與CD相交于點H,若
,BF與CD相交于點H,若![]() ,有下列結論:①
,有下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .則其中正確的結論有( )
.則其中正確的結論有( )
A. ①②③B. ①②③④C. ①②④D. ①③④
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com