【題目】某公司銷售部有營業(yè)員20人，該公司為了調動營業(yè)員的積極性，決定實行目標管理，根據目標完成的情況對營業(yè)員進行適當的獎勵，為了確定一個適當的月銷售目標，公司有關部門統(tǒng)計了這20人某月的銷售量，如下表所示：
某公司20位營業(yè)員月銷售目標統(tǒng)計表
月銷售量/件數 | 1760 | 480 | 220 | 180 | 120 | 90 |
人數 | 1 | 1 | 3 | 5 | 6 | 4 |
請根據以上提供的信息解答下列問題：
（1）求這個月中20位營業(yè)員的月銷售量的平均數；
（2）為了提高大多數營業(yè)員積極性，公司將發(fā)放A，B，C三個等級的獎金（金額：
），如果你是管理者，從平均數，中位數，眾數的角度進行分析，你將如何確定領取A，B，C級獎金各需達到的月銷售量．
科目：初中數學 來源： 題型：
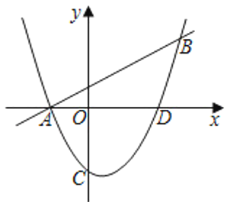
【題目】如圖，一次函數y＝
x+1的圖象與二次函數y＝x2+bx+c的圖象交于A，B兩點，點A在x軸上．點B的橫坐標為4．
（1）b＝ ，c＝ ；
（2）設二次函數的圖象與y軸交于C點，與x軸的另一個交點為D．連接AC，CD，求∠ACD的正弦值；
（3）若M點在x軸下方二次函數圖象上，
①過M點作y軸平行線交直線AB于點E，以M點為圓心，ME的長為半徑畫圓，求圓M在直線AB上截得的弦長的最大值；
②若∠ABM＝∠ACO，則點M的坐標為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有甲乙兩個玩具小汽車在筆直的240米跑道
上進行折返跑游戲，甲從點
出發(fā)，勻速在、
之間折返跑，同時乙從點出發(fā)，以大于甲的速度勻速在、之間折返跑．在折返點的時間忽略不計．
（1）若甲的速度為
，乙的速度為
，第一次迎面相遇的時間為
，則與的關系式___________；
（注釋：當兩車相向而行時相遇是迎面相遇，當兩車在點相遇時也視為迎面相遇）
（2）如圖1，
①若甲乙兩車在距點20米處第一次迎面相遇，則他們在距點_______米第二次迎面相遇：
②若甲乙兩車在距點50米處第一次迎面相遇，則他們在距點__________米第二次迎面相遇；
（3）設甲乙兩車在距點
米處第一次迎面相遇，在距點
米處第二次迎面相遇．某同學發(fā)現(xiàn)了與的函數關系，并畫出了部分函數圖象（線段
，不包括點
，如圖2所示）．
①則
_______，并在圖2中補全與的函數圖象（在圖中注明關鍵點的數據）；
②分別求出各部分圖象對應的函數表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】文化是一個國家、一個民族的靈魂，近年來，央視推出《中國詩詞大會》、《中國成語大會》、《朗讀者》、《經曲詠流傳》等一系列文化欄目．為了解學生對這些欄目的喜愛情況，某學校組織學生會成員隨機抽取了部分學生進行調查，被調查的學生必須從《經曲詠流傳》（記為A）、《中國詩詞大會》（記為B）、《中國成語大會》（記為C）、《朗讀者》（記為D）中選擇自己最喜愛的一個欄目，也可以不選以上四類而寫出一個自己最喜愛的其他文化欄目（這時記為E）．根據調查結果繪制成如圖所示的兩幅不完整的統(tǒng)計圖．
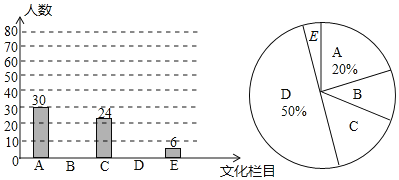
請根據圖中信息解答下列問題：
（1）在這項調查中，共調查了 名學生；
（2）最喜愛《朗讀者》的學生有 名；
（3）扇形統(tǒng)計圖中“B”所在扇形圓心角的度數為 ；
（4）選擇“E”的學生中有2名女生，其余為男生，現(xiàn)從選擇“E”的學生中隨機選出兩名學生參加座談，請直接寫出：剛好選到一名男生和一名女生的概率為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
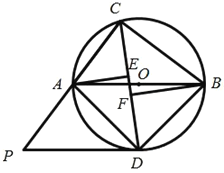
【題目】如圖，ABC內接于⊙O，AB為⊙O的直徑，∠ACB的平分線CD交⊙O于點D，過點D作⊙O的切線PD，交CA的延長線于點P，過點A作AE⊥CD于點E，過點B作BF⊥CD于點F．
（1）求證：PD//AB；
（2）求證：DE=BF；
（3）若AC=6，tan∠CAB=
，求線段PC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
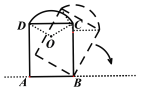
【題目】如圖，豎直放置的一個鋁合金窗框由矩形和弧形兩部分組成，AB=
m，AD= 2m，弧CD所對的圓心角為∠COD=120°．現(xiàn)將窗框繞點B順時針旋轉橫放在水平的地面上，這一過程中，窗框上的點到地面的最大高度為__m．
查看答案和解析>>
科目：初中數學 來源： 題型：
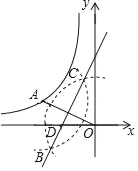
【題目】如圖，點A在反比例函數
(x<0)的圖象上，連接OA，分別以點O和點A為圓心，大于
的長為半徑作弧，兩弧相交于B，C兩點，過B，C兩點作直線交x軸于點D，連接AD．若∠AOD＝30°，△AOD的面積為2，則k的值為（ ）
A.﹣6B.6C.﹣2D.﹣3
查看答案和解析>>
科目：初中數學 來源： 題型：
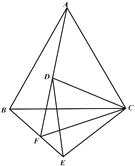
【題目】在學習《圓》這一單元時，我們學習了圓周角定理的推論：圓內接四邊形的對角互補；事實上，它的逆命題：對角互補的四邊形的四個頂點共圓，也是一個真命題．在圖形旋轉的綜合題中經常會出現(xiàn)對角互補的四邊形，那么，我們就可以借助“對角互補的四邊形的四個頂點共圓”，然后借助圓的相關知識來解決問題，例如：
已知：
是等邊三角形，點
是內一點，連接
，將線段繞
逆時針旋轉
得到線段
，連接
，
，
，并延長交于點
．當點在如圖所示的位置時：
（1）觀察填空：
①與
全等的三角形是________；
②
的度數為
（2）利用題干中的結論，證明：，，，
四點共圓；
（3）直接寫出線段
，
，
之間的數量關系．____________________．
查看答案和解析>>
科目：初中數學 來源： 題型：
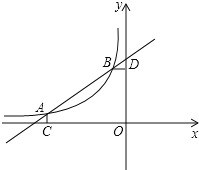
【題目】如圖，已知A(﹣3，
)，B(﹣1，m)是一次函數y＝kx+b與反比例函數y＝
圖象的兩個交點，AC⊥x軸于點C，BD⊥y軸于點D．
（1）求m的值及一次函數解析式；
（2）P是線段AB上的一點，連接PC，PD，若△PCA和△PDB面積相等，求點P坐標．
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
