
如圖,在平面直角坐標系中有一矩形ABCO(O為原點),點A、C分別在x軸、y軸上,且C點坐標為(0,6),將△BCD沿BD折疊(D點在OC邊上),使C點落在DA邊的E點上,并將△BAE沿BE折疊,恰好使點A落在BD邊的F點上.
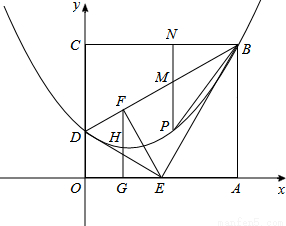
(1)求BC的長,并求折痕BD所在直線的函數解析式;
(2)過點F作FG⊥x軸,垂足為G,FG的中點為H,若拋物線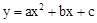 經過B,H, D三點,求拋物線解析式;
經過B,H, D三點,求拋物線解析式;
(3)點P是矩形內部的點,且點P在(2)中的拋物線上運動(不含B, D點),過點P作PN⊥BC,分別交BC 和 BD于點N, M,是否存在這樣的點P,使 如果存在,求出點P的坐標;如果不存在,請說明理由.
如果存在,求出點P的坐標;如果不存在,請說明理由.
解:(1)由翻折可知:△BCD≌△BED,∴∠CBD=∠DBE。
又∵△ABE≌△FBE,∴∠DBE=∠ABE。
又∵四邊形OCBA為矩形,∴∠CBD=∠DBE=∠ABE=30°。
在Rt△DOE中,∠ODE=60°,∴DE=CD=2OD。
∵OC=OD+CD=6,∴OD+2OD=6,∴OD=2,D(0,2)。∴CD=4。
在Rt△CDB中,BC=CD•tan60°=4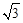 ,∴B(4
,∴B(4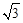 ,6)。
,6)。
設直線BD的解析式為y=kx+b,由題意得: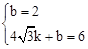 ,解得
,解得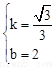 。
。
∴直線BD的解析式為: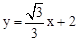 。
。
(2)在Rt△FGE中,∠FEG=60°,FE=AE.
由(1)易得:OE=2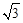 ,∴FE=AE=2
,∴FE=AE=2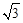 。
。
∴FG=3,GE=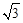 。∴OG=
。∴OG=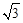 。
。
∵H是FG的中點,∴H(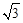 ,
,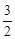 )。
)。
∵拋物線 經過B、H、D三點,
經過B、H、D三點,
∴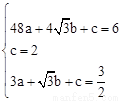 ,解得
,解得 。
。
∴拋物線解析式為 。
。
(3)存在。
∵P在拋物線上,∴設P(x,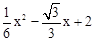 ),M(x,
),M(x, ),N(x,6)。
),N(x,6)。
∵S△BNM=S△BPM,∴PM=MN.即: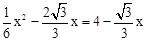 。
。
整理得: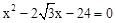 ,解得:x=2
,解得:x=2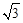 或x=4
或x=4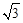 。
。
當x=2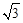 時,
時,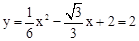 ;
;
當x=4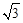 時,
時,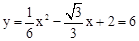 ,與點B重合,不符合題意,舍去。
,與點B重合,不符合題意,舍去。
∴P(2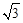 ,2)。
,2)。
∴存在點P,使S△BNM=S△BPM,點P的坐標為(2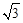 ,2)。
,2)。
【解析】
試題分析:(1)首先由折疊性質得到∠CBD=∠DBE=∠ABE=30°,然后解直角三角形得到點D、點B的坐標,最后用待定系數法求出直線BD的解析式;
(2)點B、D坐標已經求出,關鍵是求出點H的坐標.在Rt△FGE中,解直角三角形求出點H的坐標,再利用待定系數法求出拋物線的解析式。
(3)由S△BNM=S△BPM,且這兩個三角形等高,所以得到PM=MN.由此結論,列出方程求出點P的坐標。


科目:初中數學 來源: 題型:
 如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD.
如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是
(2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=
如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 ∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.
∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com