
【題目】如圖所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜邊DF上一動點,過B作AB⊥DF于B,交邊DE(或邊EF)于點A,設BD=x,△ABD的面積為y,則y與x之間的函數圖象大致為( )
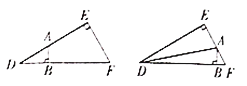

A. (A) B. (B) C. (C) D. (D)
【答案】B
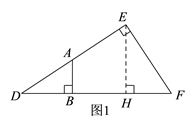
【解析】如圖1和圖2,過點E作EH⊥DF于點H,
∵在△DEF中,∠DEF=90°,∠D=30°,DF=16,
∴EF=8,DE=![]() ,EH=
,EH=![]() ,DH=12,HF=4,
,DH=12,HF=4,
(1)如圖1,當點A在DE上時,此時點B在DH上,即![]() ,
,
∵AB⊥DF于點B,∠D=30°,BD= ![]() ,
,
∴AB=BD·tan∠D= ![]() ,
,
∴此時y=S△ABD= =![]() ,即
,即![]() ,
,
∴當![]() 時,y有最大值,此時點A與E重合;
時,y有最大值,此時點A與E重合;
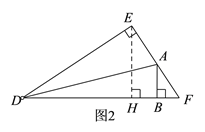
(2)如圖2,當點A在EF上時,此時點B在HF上,即![]() ,
,
∵AB⊥DF于點B,∠D=30°,BD= ![]() ,
,
∴BF= ![]() ,∠ABF=90°,∠F=60°,
,∠ABF=90°,∠F=60°,
∴AB=BF·tan∠F=![]() ,
,
∴此時y=S△ABD=![]() BD·AB=
BD·AB=![]() ,即y=
,即y= ![]() ;
;
綜上所述,結合二次函數的圖象特征可知y隨x變化而變化的圖象應該是B選項中的圖象.
故選B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
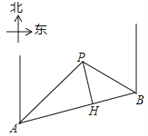
【題目】某條道路上通行車輛限速60千米/時,道路的AB段為監測區,監測點P到AB的距離PH為50米(如圖).已知點P在點A的北偏東45°方向上,且在點B的北偏西60°方向上,點B在點A的北偏東75°方向上,那么車輛通過AB段的時間在多少秒以內,可認定為超速?(參考數據:![]() ≈1.7,
≈1.7,![]() ≈1.4).
≈1.4).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知輪船A在燈塔P的北偏東30°的方向上,輪船B在燈塔P的南偏東70°的方向上.
(1)求從燈塔P看兩輪船的視角(即∠APB)的度數?
(2)輪船C在∠APB的角平分線上,則輪船C在燈塔P的什么方位?

查看答案和解析>>
科目:初中數學 來源: 題型:
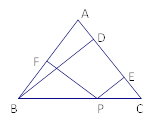
【題目】如圖,在△ABC中,AB=AC,P為BC邊上任意一點,PF⊥AB于F,PE⊥AC于E,若AC邊上的高BD=a.
(1)試說明PE+PF=a;
(2)若點P在BC的延長線上,其它條件不變,上述結論還成立嗎?如果成立請說明理由;如果不成立,請重新給出一個關于PE,PF,a的關系式,不需要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,海中有一小島P,在距小島P的![]() 海里范圍內有暗礁,一輪船自西向東航行,它在A處時測得小島P位于北偏東60°,且A、P之間的距離為32海里,若輪船繼續向正東方向航行,輪船有無觸礁危險?請通過計算加以說明.如果有危險,輪船自A處開始至少沿東偏南多少度方向航行,才能安全通過這一海域?
海里范圍內有暗礁,一輪船自西向東航行,它在A處時測得小島P位于北偏東60°,且A、P之間的距離為32海里,若輪船繼續向正東方向航行,輪船有無觸礁危險?請通過計算加以說明.如果有危險,輪船自A處開始至少沿東偏南多少度方向航行,才能安全通過這一海域?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索發現:
(1)計算:當a 4, b 3時, a2 b2 ; (a b)(a b) 。
當a 1, b 2 時, a2 b2 ; (a b)(a b) 。
(2)你能從上面的計算中發現什么結論? 。
(3)利用你發現的結論,求![]() 的值。
的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
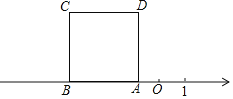
【題目】如圖,正方形ABCD的邊AB在數軸上,數軸上點A表示的數為﹣1,正方形ABCD的面積為a2(a>1).將正方形ABCD在數軸上水平移動,移動后的正方形記為A′B′C′D′,點A、B、C、D的對應點分別為A′、B′、C′、D′,移動后的正方形A′B′C′D′與原正方形ABCD重疊部分圖形的面積記為S.當S=a時,數軸上點A′表示的數是_____.(用含a的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 的意義是數軸上表示x、y 的兩點之間的距離。例如:
的意義是數軸上表示x、y 的兩點之間的距離。例如:![]() 表示4與 —2 的差的絕對值,實際上也可以理解為 4 與—2 兩數在數軸上所對應的兩點之間的距離;同理
表示4與 —2 的差的絕對值,實際上也可以理解為 4 與—2 兩數在數軸上所對應的兩點之間的距離;同理![]() 也可以理解為 x 與 3 兩數在數軸上所對應的兩點之間的距離。試探索:
也可以理解為 x 與 3 兩數在數軸上所對應的兩點之間的距離。試探索:
(1)![]() = ;
= ;
(2)若![]() ,則 x= ;
,則 x= ;
(3)請你找出符合條件的整數x ,使得![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com