
【題目】如圖,∠AOB=∠DOC=90°,OE平分∠AOD,反向延長射線OE至F.
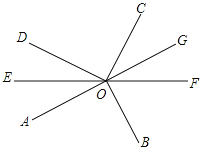
(1)∠AOD和∠BOC是否互補?說明理由;
(2)射線OF是∠BOC的平分線嗎?說明理由;
(3)反向延長射線OA至點G,射線OG將∠COF分成了4:3的兩個角,求∠AOD.
【答案】(1)互補;理由見解析;(2)是;理由見解析;(3)54°或![]()
【解析】
(1)根據和等于180°的兩個角互補即可求解;
(2)通過求解得到∠COF=∠BOF,根據角平分線的定義即可得出結論;
(3)分兩種情況:①當∠COG:∠GOF=4:3時;②當∠COG:∠GOF=3:4時;進行討論即可求解.
(1)因為∠AOD+∠BOC=360°﹣∠AOB﹣∠DOC=360°﹣90°﹣90°=180°,
所以∠AOD和∠BOC互補.
(2)因為OE平分∠AOD,所以∠AOE=∠DOE,
因為∠COF=180°﹣∠DOC﹣∠DOE=90°﹣∠DOE,
∠BOF=180°﹣∠AOB﹣∠AOE=90°﹣∠AOE,
所以∠COF=∠BOF,即OF是∠BOC的平分線.
(3)因為OG將∠COF分成了4:3的兩個部分,
所以∠COG:∠GOF=4:3或者∠COG:∠GOF=3:4.
①當∠COG:∠GOF=4:3時,設∠COG=4x°,則∠GOF=3x°,
由(2)得:∠BOF=∠COF=7x°
因為∠AOB+∠BOF+∠FOG=180°,
所以90°+7x+3x=180°,
解方程得:x=9°,
所以∠AOD=180°﹣∠BOC=180°﹣14x=54°.
②當∠COG:∠GOF=3:4時,設∠COG=3x°,∠GOF=4x°,
同理可列出方程:90°+7x+4x=180°,
解得:x = ![]() ,
,
所以∠AOD=180°﹣∠BOC=180°﹣14x![]() .
.
綜上所述:∠AOD的度數是54°或![]() .
.


科目:初中數學 來源: 題型:
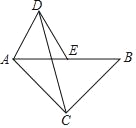
【題目】如圖,在等腰Rt△ABC中,∠ACB=90°,AB=4,點E為AB的中點.以AE為邊作等邊△ADE(點D與點C分別在AB的異側),連接CD.則△ACD的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,觀察函數y=|x|的圖象,寫出它的兩條的性質;
(2)在圖1中,畫出函數y=|x-3|的圖象;
根據圖象判斷:函數y=|x-3|的圖象可以由y=|x|的圖象向 平移 個單位得到;
(3)①函數y=|2x+3|的圖象可以由y=|2x|的圖象向 平移 單位得到;
②根據從特殊到一般的研究方法,函數y=|kx+3|(k為常數,k≠0)的圖象可以由函數y=|kx|(k為常數,k≠0)的圖象經過怎樣的平移得到.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)(﹣8)﹣(﹣15)+(﹣9)﹣(﹣12)
(2)7![]() +(﹣6.5)+3
+(﹣6.5)+3![]() +(﹣1.25)+2
+(﹣1.25)+2![]()
(3)(﹣81)÷(﹣2![]() )×
)×![]() ÷(﹣8)
÷(﹣8)
(4)![]()
(5)![]()
(6)![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前,步行已成為人們最喜愛的健身方法之一,通過手機可以計算行走的步數與相應的能量消耗.對比手機數據發現:小瓊步行![]() 步與小剛步行
步與小剛步行![]() 步消耗的能量相同,若每消耗
步消耗的能量相同,若每消耗![]() 千卡能量小瓊行走的步數比小剛多
千卡能量小瓊行走的步數比小剛多![]() 步,求小剛每消耗
步,求小剛每消耗![]() 千卡能量需要行走多少步?
千卡能量需要行走多少步?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖O為直線AB上一點,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度數;
(2)試判斷OE是否平分∠BOC,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場將進價為2000元的冰箱以2400元售出,平均每天能售出8臺,為了配合國家“家電下鄉”政策的實施,商場決定采取適當的降價措施.調查表明:這種冰箱的售價每降低50元,平均每天就能多售出4臺.
(1)假設每臺冰箱降價x元,商場每天銷售這種冰箱的利潤是y元,請寫出y與x之間的函數表達式;(不要求寫自變量的取值范圍)
(2)商場要想在這種冰箱銷售中每天盈利4800元,同時又要使百姓得到實惠,每臺冰箱應降價多少元?
(3)每臺冰箱降價多少元時,商場每天銷售這種冰箱的利潤最高?最高利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 的邊
的邊![]() 上有一動點
上有一動點![]() ,從距離
,從距離![]() 點
點![]() 的點
的點![]() 處出發,沿線段
處出發,沿線段![]() ,射線
,射線![]() 運動,速度為
運動,速度為![]() ;動點
;動點![]() 從點
從點![]() 出發,沿射線
出發,沿射線![]() 運動,速度為
運動,速度為![]() .
.![]() ,
,![]() 同時出發,設運動時間是
同時出發,設運動時間是![]() .
.

(1)當點![]() 在
在![]() 上運動時,
上運動時,![]()
![]() (用含
(用含![]() 的代數式表示);
的代數式表示);
(2)當點![]() 在
在![]() 上運動時,
上運動時,![]() 為何值,能使
為何值,能使![]() ?
?
(3)若點![]() 運動到距離
運動到距離![]() 點
點![]() 的點
的點![]() 處停止,在點
處停止,在點![]() 停止運動前,點
停止運動前,點![]() 能否追上點
能否追上點![]() ?如果能,求出
?如果能,求出![]() 的值;如果不能,請說出理由.
的值;如果不能,請說出理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com