(1)①CF=BD CF⊥BD,
解:結論還成立,CF=BD CF⊥BD,
理由是:∵四邊形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中
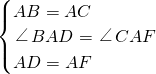
,
∴△BAD≌△CAF,
∴CF=BD,∠B=∠ACF,
∵∠BAC=90°,
∴∠B+∠BCA=90°,
∴∠ACF+∠ACB=90°,
∴CF⊥BD,
故答案為:CF=BD,CF⊥BD.
②解:結論還成立,
理由是由①知,∠BAC=FAD=90°,
∴∠BAC+∠CAD=∠FAD+∠CAD,
∴∠BAD=∠FAC,
∵在△BAD和△CAF中
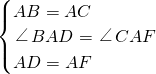
,
∴△BAD≌△CAF,
∴CF=BD,∠B=∠ACF,
∵∠BAC=90°,
∴∠B+∠BCA=90°,
∴∠ACF+∠ACB=90°,
∴CF⊥BD,
即①的結論還成立.
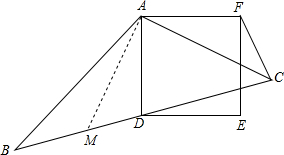
(2)解:當∠ACB=45°時,CF⊥BD
理由是:如圖1,當∠BAC>90°,過點A作AM⊥CA交BC于M,
則AM=AC,
由(1)同理可證明△FAC≌△MAD,
∴∠ACF=∠AMD=45°,
∴∠FCB=90°,
即CF⊥BD.
分析:(1)①根據正方形和等邊三角形的性質得出AD=AF,∠BAC=∠DAF=90°,求出∠BAD=∠CAF,證△BAD≌△CAF,推出BD=CF,∠B=∠ACF,求出∠FCB=90°即可;
②求出∠BAD=∠CAF,證△BAD≌△CAF,推出BD=CF,∠B=∠ACF,求出∠FCB=90°即可;
(2)在BD上截取AM=AC,連接AM,與(1)證明過程類似證MAD≌△CAF即可求出答案.
點評:本題考查了全等三角形的性質和判定,正方形的性質,主要培養學生的推理能力,本題具有一定的代表性,證明過程類似,透過做此題培養了學生的發散思維能力.


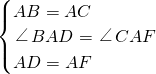 ,
,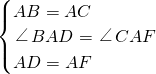 ,
, (2)解:當∠ACB=45°時,CF⊥BD
(2)解:當∠ACB=45°時,CF⊥BD

 口算能手系列答案
口算能手系列答案 如圖所示,在△ABC中,AC與⊙O相切于點A,AC=AB=2,⊙O交BC于D.
如圖所示,在△ABC中,AC與⊙O相切于點A,AC=AB=2,⊙O交BC于D. (2013•松江區二模)如圖,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江區二模)如圖,已知在△ABC中,AC=15,AB=25,sin∠CAB=