
【題目】已知![]() 為直線
為直線![]() 上的一點,
上的一點,![]() 是直角,
是直角,![]() 平分
平分![]() .
.
(1)如圖1,若![]() =
=![]() °,則
°,則![]() = °,
= °,![]() 與
與![]() 的數量關系為 .
的數量關系為 .
(2)當射線![]() 繞點
繞點![]() 逆時針旋轉到如圖2的位置時,(1)中
逆時針旋轉到如圖2的位置時,(1)中![]() 與
與![]() 的關系是否仍然成立?如成立,請說明理由.
的關系是否仍然成立?如成立,請說明理由.
(3)在圖3中,若![]() =
=![]() °,在
°,在![]() 的內部是否存在一條射線
的內部是否存在一條射線![]() ,使得
,使得![]() ?若存在,請求出
?若存在,請求出![]() 的度數;若不存在,請說明理由.
的度數;若不存在,請說明理由.

【答案】(1)56°;∠BOE=2∠COF;(2) ∠BOE=2∠COF仍然成立,理由見解析;(3)存在,∠BOD=16°.
【解析】
(1)由題意可知:∠FOE=90°∠COF,由角平分線的性質可求得∠AOE=2∠EOF,所以∠BOE=180°∠AOE,即可求得答案,設∠COF=n°,同理可得∠BOE=2∠COF;
(2)設∠COF=n°,故∠EOF=90°n,由角平分線的性質即可求得∠AOE=180°2n°,從而求得∠BOE與∠COF的數量關系;
(3)由(2)可知:∠BOE=2∠COF=130°,進而求得∠AOE=180°∠BOE=50°,由于OF平分∠AOE,所以∠AOF=![]() ∠AOE=25°,分別代入2∠BOD+∠AOF=
∠AOE=25°,分別代入2∠BOD+∠AOF=![]() (∠BOE∠BOD)解得∠BOD即可.
(∠BOE∠BOD)解得∠BOD即可.
解:(1)∵∠COE是直角,∠COF=28°,
∴∠EOF=90°∠COF=62°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=124°,
∴∠BOE=180°∠AOE=56°,
若∠COF=n°,則∠EOF=90° n°,
∴∠AOE=2∠EOF=180° 2n°,
∴∠BOE=180°∠AOE=2n°,
∴∠BOE=2∠COF;
(2)∠BOE=2∠COF仍然成立,
理由:設∠COF=n°,
∴∠EOF=90°∠COF=90°n°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=180°2n°,
∴∠BOE=180°∠AOE=2n°=2∠COF,
故∠BOE與∠COF的關系是仍然成立;
(3)由(2)可知:∠BOE=2∠COF=130°,
∴∠AOE=180°∠BOE=50°,
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=25°,
∠AOE=25°,
∵2∠BOD+∠AOF=![]() (∠BOE∠BOD),
(∠BOE∠BOD),
∴2∠BOD+25°=![]() (130°∠BOD)
(130°∠BOD)
解得:∠BOD=16°.


科目:初中數學 來源: 題型:
【題目】如圖,在同一平面內四個點A,B,C,D.
(1)利用尺規,按下面的要求作圖.要求:不寫畫法,保留作圖痕跡,不必寫結論.
①作射線AC;
②連接AB,BC,BD,線段BD與射線AC相交于點O;
③在線段AC上作一條線段CF,使CF=AC﹣BD.
(2)觀察(1)題得到的圖形,我們發現線段AB+BC>AC,得出這個結論的依據是 .
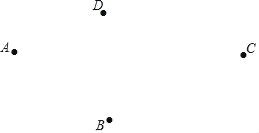
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(12分)如圖,已知三角形ABC的邊AB是⊙O的切線,切點為B.AC經過圓心O并與圓相交于點D、C,過C作直線CE丄AB,交AB的延長線于點E.

(1)求證:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:![]() (
(![]() 、
、![]() 是正整數,且
是正整數,且![]() ).在n的所有這種分解中,如果
).在n的所有這種分解中,如果![]() 、
、![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是n的最佳分解,并規定:
是n的最佳分解,并規定:![]() .例如12可以分解成
.例如12可以分解成![]() ,
,![]() 或
或![]() ,因為
,因為![]() ,所以
,所以![]() 是12的最佳分解,所以
是12的最佳分解,所以![]() .如果一個兩位正整數
.如果一個兩位正整數![]() ,
,![]() (
(![]() ,
,![]() 、
、![]() 為正整數),交換其個位上的數字與十位上的數字得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數
為正整數),交換其個位上的數字與十位上的數字得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數![]() 為“吉祥數”,則所有“吉祥數”中
為“吉祥數”,則所有“吉祥數”中![]() 的最大值為_____________.
的最大值為_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是用大小相等的小五角星按一定規律拼成的一組圖案,第1個圖案中有4顆五角星,第2個圖案中有7顆五角星,第3個圖案中有10顆五角星,…,請根據你的觀察完成下列問題.

(1)根據上述規律,分別寫出第4個圖案和第5個圖案中小五角星的顆數;
(2)按如圖所示的規律,求出第![]() 個圖案中小五角星的顆數(用含
個圖案中小五角星的顆數(用含![]() 的代數式表示);
的代數式表示);
(3)求第2019個圖案中小五角星的顆數?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:①兩個數互為倒數,則它們乘積為1;②若a、b互為相反數,則![]() =﹣1;③兩個四次單項式的和一定是四次多項式;④兩個有理數比較,絕對值大的反而小;⑤若a為任意有理數,則a﹣|a|≤0;⑥﹣5πR2的系數是﹣5.其中正確的有( )
=﹣1;③兩個四次單項式的和一定是四次多項式;④兩個有理數比較,絕對值大的反而小;⑤若a為任意有理數,則a﹣|a|≤0;⑥﹣5πR2的系數是﹣5.其中正確的有( )
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
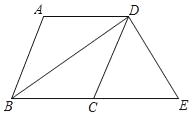
【題目】如圖,在四邊形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求證:四邊形ABCD是菱形;
(2)過點D作DE⊥BD,交BC的延長線于點E,若BC=5,BD=8,求四邊形ABED的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐵路貨運調度站有A、B兩個信號燈,在燈這旁停靠著甲、乙、丙三列火車.它們中最長的車長與居中車長之差等于居中車長與最短車長之差,其中乙車的車長居中,最開始的時候,甲、丙兩車車尾對齊,且車尾正好位于A信號燈處,而車頭則沖著B信號燈的方向,乙車的車尾則位于B信號燈處,車頭則沖著A的方向,現在,三列火車同時出發向前行駛,3秒之后三列火車的車頭恰好相遇,再過9秒,甲車恰好超過丙車,而丙車也正好完全和乙車錯開,請問:甲乙兩車從車頭相遇直到完全錯開一共用了_____秒鐘.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,當圖形W上的點P的橫坐標和縱坐標相等時,則稱點P為圖形W的“夢之點”.
(1)已知⊙O的半徑為1.
①在點E(1,1),F(![]() ,-
,-![]() ),M(-2,-2)中,⊙O的“夢之點”為 ;
),M(-2,-2)中,⊙O的“夢之點”為 ;
②若點P位于⊙O內部,且為雙曲線![]() (k≠0)的“夢之點”,求k的取值范圍.
(k≠0)的“夢之點”,求k的取值范圍.
(2)已知點C的坐標為(1,t),⊙C的半徑為![]() ,若在⊙C上存在“夢之點”P,直接寫出t的取值范圍.
,若在⊙C上存在“夢之點”P,直接寫出t的取值范圍.
(3)若二次函數![]() 的圖象上存在兩個“夢之點”
的圖象上存在兩個“夢之點”![]() ,
,![]() ,且
,且![]() ,求二次函數圖象的頂點坐標.
,求二次函數圖象的頂點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com