
 x+3與x軸相交于點A,與y軸相交于點B,點C(m,n)是第二象限內任意一點,以點C為圓心的圓與x軸相切于點E,與直線AB相切于點F.
x+3與x軸相交于點A,與y軸相交于點B,點C(m,n)是第二象限內任意一點,以點C為圓心的圓與x軸相切于點E,與直線AB相切于點F.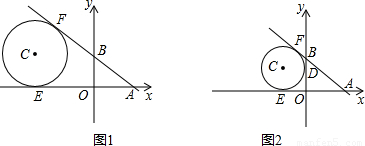
 x+3與x軸相交于點A,與y軸相交于點B,所以分別令x=0,y=0,可求出A(4,0),B(0,3),所以OA=4,OB=3,AB=5,連接CF,當四邊形OBCE為矩形時,有CF=CE=OB=3,CB∥x軸,利用兩直線平行同位角相等可得∠CBF=∠BAO,又因⊙C與直線AB相切于點F,所以CF⊥AB于點F,利用AAS可知△CBF≌△BAO,所以CB=AB=5,即點C的坐標為(-5,3);
x+3與x軸相交于點A,與y軸相交于點B,所以分別令x=0,y=0,可求出A(4,0),B(0,3),所以OA=4,OB=3,AB=5,連接CF,當四邊形OBCE為矩形時,有CF=CE=OB=3,CB∥x軸,利用兩直線平行同位角相等可得∠CBF=∠BAO,又因⊙C與直線AB相切于點F,所以CF⊥AB于點F,利用AAS可知△CBF≌△BAO,所以CB=AB=5,即點C的坐標為(-5,3); (AB+OA+OB)=6,又因由切線性質定理得,CE⊥x軸于點E,CD⊥y軸于點D,所以四邊形CEOD為矩形,又因為CE=CD,所以四邊形CEOD為正方形,所以OE=CE=r=AE-OA=6-4=2;
(AB+OA+OB)=6,又因由切線性質定理得,CE⊥x軸于點E,CD⊥y軸于點D,所以四邊形CEOD為矩形,又因為CE=CD,所以四邊形CEOD為正方形,所以OE=CE=r=AE-OA=6-4=2;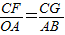 ,即CG=
,即CG= n,又因GE=CG+CE=
n,又因GE=CG+CE=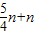 =
= n,AE=OA+OE=4-m,利用tan∠EAG=tan∠BAO,即可得到關于m、n的關系式
n,AE=OA+OE=4-m,利用tan∠EAG=tan∠BAO,即可得到關于m、n的關系式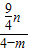 =
= ,整理即可;
,整理即可;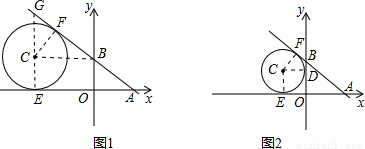
 (AB+OA+OB)=6,
(AB+OA+OB)=6,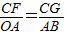 ,
, n,
n,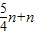 =
= n,
n,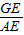 =
=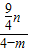 ,
,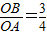 ,
, =
= ,
,

科目:初中數學 來源:2005年全國中考數學試題匯編《反比例函數》(05)(解析版) 題型:解答題
 (x<0)分別交于點C、D,且C點的坐標為(-1,2).
(x<0)分別交于點C、D,且C點的坐標為(-1,2).
查看答案和解析>>
科目:初中數學 來源:2005年全國中考數學試題匯編《一次函數》(05)(解析版) 題型:解答題
 ,∠CAO=30度.將Rt△OAC折疊,使OC邊落在AC邊上,點O與點D重合,折痕為CE.
,∠CAO=30度.將Rt△OAC折疊,使OC邊落在AC邊上,點O與點D重合,折痕為CE.
查看答案和解析>>
科目:初中數學 來源:2010年四川省成都市武侯區中考數學一模試卷(解析版) 題型:解答題
 (x<0)分別交于點C、D,且C點的坐標為(-1,2).
(x<0)分別交于點C、D,且C點的坐標為(-1,2).
查看答案和解析>>
科目:初中數學 來源:2005年遼寧省沈陽市中考數學試卷(課標卷)(解析版) 題型:解答題
 ,∠CAO=30度.將Rt△OAC折疊,使OC邊落在AC邊上,點O與點D重合,折痕為CE.
,∠CAO=30度.將Rt△OAC折疊,使OC邊落在AC邊上,點O與點D重合,折痕為CE.
查看答案和解析>>
科目:初中數學 來源:2005年遼寧省沈陽市中考數學試卷(大綱卷)(解析版) 題型:解答題
 (x<0)分別交于點C、D,且C點的坐標為(-1,2).
(x<0)分別交于點C、D,且C點的坐標為(-1,2).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com