
如圖,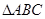 中,
中,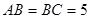 ,
,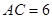 ,過點
,過點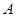 作
作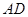 ∥
∥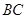 ,點
,點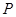 、
、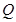 分別是射線
分別是射線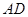 、線段
、線段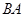 上的動點,且
上的動點,且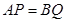 ,過點
,過點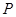 作
作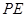 ∥
∥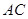 交線段
交線段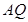 于點
于點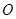 ,聯接
,聯接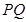 ,設
,設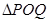 面積為
面積為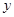 ,
,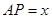 .
.
(1)用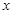 的代數式表示
的代數式表示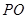 ;
;
(2)求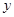 與
與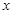 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(3)聯接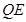 ,若
,若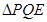 與
與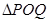 相似,求
相似,求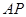 的長.
的長.

(1)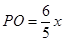 (2)
(2)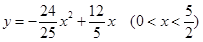 (3)
(3)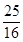
【解析】(1)∵ ∥
∥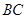 ,
,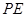 ∥
∥ ,
,
∴四邊形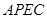 是平行四邊形
1分
是平行四邊形
1分
∴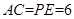 ,
,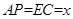 1分
1分
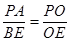 ,
,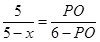 1分
1分
可得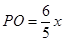 1分
1分
解:(2)∵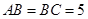 ,
,
∴∠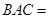 ∠
∠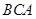
又∠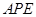 =∠
=∠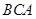 ,∠
,∠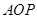 =∠
=∠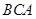 ,
,
∴∠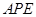 =∠
=∠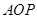 ,
,
∴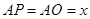 源:學*科*網]
源:學*科*網]
∴當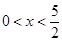 時,
時,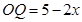 ;
1分
;
1分
作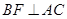 ,
,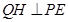 ,垂足分別為點
,垂足分別為點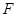 、
、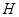 ,
,

則易得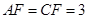 ,
,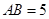 ,
,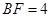 ,
,
由∠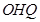 =∠
=∠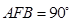 ,∠
,∠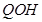 =∠
=∠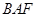
得△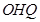 ∽△
∽△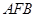
∴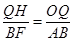 ,
,
∴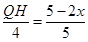 ,
,
∴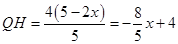 2分
2分
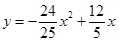 1分
1分
所以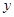 與
與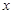 的函數關系式是
的函數關系式是
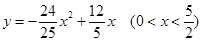 1分
1分
解:(3)【解法一】當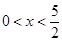 時
時
由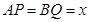 ,
,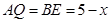 ,∠
,∠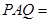 ∠
∠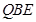
可得△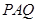 ≌△
≌△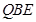 ,于是
,于是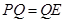 1分
1分
由于∠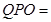 ∠
∠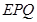 ,
,
所以若△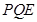 與△
與△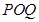 相似,
相似,
只有△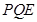 ∽△
∽△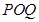
可得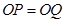 1分
1分
于是得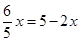 ,解得
,解得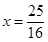 2分
2分
同理當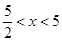 ,可得
,可得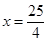 (不合題意,舍去) 1分
(不合題意,舍去) 1分
所以,若△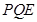 與△POQ相似,AP的長為
與△POQ相似,AP的長為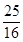 。
。
【解法二】當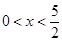 時,可得
時,可得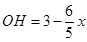 ,
,
于是得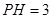 ,
,
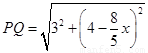 1分
1分
由于∠ =∠
=∠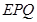 ,
,
所以若△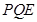 與△
與△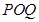 相似,只有△
相似,只有△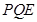 ∽△
∽△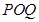
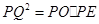 1分
1分
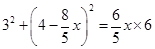
解得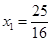 ,
,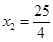 (不合題意,舍去) 2分
(不合題意,舍去) 2分
所以,若△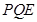 與△
與△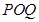 相似,
相似,
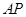 的長為
的長為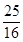 1分
1分
(1)首先根據AD∥BC,PE∥AC,判定四邊形APEC是平行四邊形,從而得到AC=PE=6,AP=EC=x,然后根據平行線分線段成比例定理列出比例式用含x的代數式表示PO;
(2)根據AB=BC=5,利用等邊對等角得到∠BAC=∠BCA,再根據∠APE=∠BCA,∠AOP=∠BCA,得到∠APE=∠AOP,設AP=AO=x,用含x的式子表示OQ=5-2x,利用△OHQ∽△AFB表示出y與x的函數關系式即可;
(3)根據當0<x<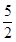 時,由AP=BQ=x,AQ=BE=5-x,∠PAQ=∠QBE可得△PAQ≌△QBE,于是PQ=QE,可得若△PQE與△POQ相似,只有△PQE∽△POQ,于是得
時,由AP=BQ=x,AQ=BE=5-x,∠PAQ=∠QBE可得△PAQ≌△QBE,于是PQ=QE,可得若△PQE與△POQ相似,只有△PQE∽△POQ,于是得 x=5-2x,解得x的值即可.
x=5-2x,解得x的值即可.
|


科目:初中數學 來源:2012屆上海市金山初三二模數學試卷(帶解析) 題型:解答題
如圖,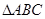 中,
中,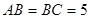 ,
,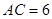 ,過點
,過點 作
作 ∥
∥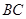 ,點
,點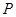 、
、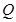 分別是射線
分別是射線 、線段
、線段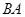 上的動點,且
上的動點,且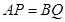 ,過點
,過點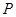 作
作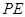 ∥
∥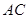 交線段
交線段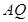 于點
于點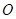 ,聯接
,聯接 ,設
,設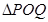 面積為
面積為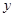 ,
, .
.
(1)用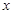 的代數式表示
的代數式表示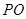 ;
;
(2)求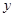 與
與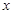 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(3)聯接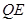 ,若
,若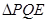 與
與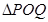 相似,求
相似,求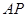 的長.
的長.
查看答案和解析>>
科目:初中數學 來源:2012-2013學年浙江省八里店一中九年級第二學期期中考試數學試卷(帶解析) 題型:解答題
如圖,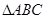 中,
中, ,
,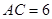 ,過點
,過點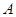 作
作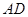 ∥
∥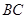 ,點
,點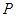 、
、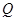 分別是射線
分別是射線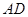 、線段
、線段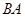 上的動點,且
上的動點,且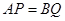 ,過點
,過點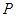 作
作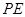 ∥
∥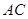 交線段
交線段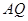 于點
于點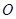 ,聯接
,聯接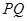 ,設
,設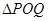 面積為
面積為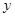 ,
,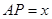 .
.
(1)用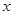 的代數式表示
的代數式表示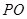 ;
;
(2)求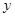 與
與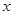 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(3)聯接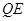 ,若
,若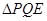 與
與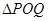 相似,求
相似,求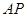 的長.
的長.
查看答案和解析>>
科目:初中數學 來源:2013屆浙江省九年級第二學期期中考試數學試卷(解析版) 題型:解答題
如圖,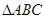 中,
中,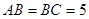 ,
,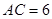 ,過點
,過點 作
作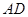 ∥
∥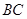 ,點
,點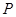 、
、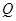 分別是射線
分別是射線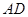 、線段
、線段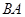 上的動點,且
上的動點,且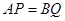 ,過點
,過點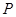 作
作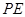 ∥
∥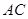 交線段
交線段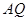 于點
于點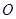 ,聯接
,聯接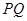 ,設
,設 面積為
面積為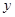 ,
,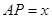 .
.

(1)用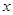 的代數式表示
的代數式表示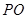 ;
;
(2)求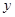 與
與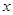 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(3)聯接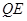 ,若
,若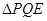 與
與 相似,求
相似,求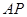 的長.
的長.
查看答案和解析>>
科目:初中數學 來源:2010-2011學年南京市考數學一模試卷 題型:解答題
(本題12分) 在正方形網格中以點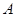 為圓心,
為圓心,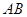 為半徑作圓
為半徑作圓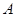 交網格于點
交網格于點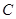 (如圖(1)),過點
(如圖(1)),過點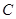 作圓的切線交網格于點
作圓的切線交網格于點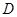 ,以點
,以點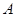 為圓心,
為圓心,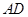 為半徑作圓交網格于點
為半徑作圓交網格于點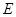
(如圖(2)).
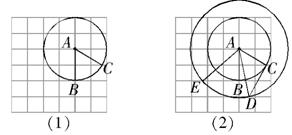
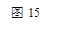 問題:
問題:
(1)求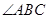 的度數;
的度數;
(2)求證: 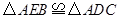 ;
;
(3)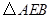 可以看作是由
可以看作是由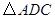 經過怎樣的變換得到的?并判斷
經過怎樣的變換得到的?并判斷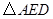 的形狀(不用說明理由).
的形狀(不用說明理由).
(4)如圖(3),已知直線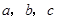 ,且a∥b,b∥c,在圖中用直尺、三角板、圓規畫等邊三角形
,且a∥b,b∥c,在圖中用直尺、三角板、圓規畫等邊三角形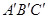 ,使三個頂點
,使三個頂點 ,分別在直線
,分別在直線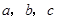 上.要求寫出簡要的畫圖過程,不需要說明理由.
上.要求寫出簡要的畫圖過程,不需要說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com