
 已知拋物線y=ax2+bx+c(a>0)的圖象經過點B(14,0)和C(0,-8),對稱軸為x=4.
已知拋物線y=ax2+bx+c(a>0)的圖象經過點B(14,0)和C(0,-8),對稱軸為x=4.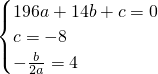 ,
,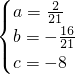 ,
, x2-
x2- x-8;
x-8; x2-
x2- x-8=0,
x-8=0,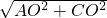 =
= =10,
=10, AC=
AC= ×10=5,
×10=5,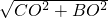 =
= =2
=2 ,
, BC=
BC= ×2
×2 =
= ,
,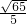 單位長度.
單位長度. AC,再求出AP,然后根據時間=路程÷速度求出點P運動的時間t,根據勾股定理求出BC,然后求出CQ,根據速度=路程÷時間,計算即可求出點Q的速度.
AC,再求出AP,然后根據時間=路程÷速度求出點P運動的時間t,根據勾股定理求出BC,然后求出CQ,根據速度=路程÷時間,計算即可求出點Q的速度.

科目:初中數學 來源: 題型:
 與x軸的另一個交點為E.
與x軸的另一個交點為E.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=
如圖,已知拋物線y=ax2+bx+c(其中b>0,c<0)的頂點P在x軸上,與y軸交于點Q,過坐標原點O,作OA⊥PQ,垂足為A,且OA=| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| c | a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com