
��D�����タ �c
�c �S�ཻ���c
�S�ཻ���c ����1��0����
����1��0���� ��3��0�����c
��3��0�����c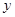 �S�ཻ���c
�S�ཻ���c ���c
���c �龀��
�龀�� �ϵĄ��c�����c
�ϵĄ��c�����c ��
�� �غϣ����^�c
�غϣ����^�c ��ֱ��
��ֱ�� �S��ֱ���c���タ������
�S��ֱ���c���タ������ �քe�����c
�քe�����c ��
�� ���c
���c ��
��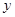 �S�����S�ϣ�
�S�����S�ϣ� =2���B��
=2���B�� ��
�� ��
��
��1�����タ�Ľ���ʽ��
��2������߅�� ��ƽ����߅�Εr�����c
��ƽ����߅�Εr�����c �����ˣ�
�����ˣ�
��3���^�c ��ֱ������2���е�ƽ����߅��
��ֱ������2���е�ƽ����߅�� �ֳ���e��ȵăɲ��֣����@�lֱ���Ľ���ʽ���������f��ƽ��ƽ����߅����e�����ɣ�
�ֳ���e��ȵăɲ��֣����@�lֱ���Ľ���ʽ���������f��ƽ��ƽ����߅����e�����ɣ�
��1�����タ�Ľ���ʽ�飺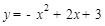 ��(2)
��(2) �c���˞�
�c���˞�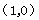 ��
��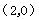 ��(3) �ٮ�
��(3) �ٮ�
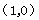 �r������ֱ���Ľ���ʽ�飺
�r������ֱ���Ľ���ʽ�飺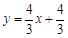 ���ڮ�
���ڮ�
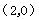 �r������ֱ���Ľ���ʽ�飺
�r������ֱ���Ľ���ʽ�飺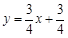 .
.
����ԇ�}������
��1�����c ���c
���c �����˴��뒁�タ����(sh��)�У������δ֪��
�����˴��뒁�タ����(sh��)�У������δ֪��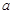 ��
��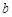 .�t�����ԓ���タ����ʽ����2����ƽ����߅�ε����|(zh��)��֪��
.�t�����ԓ���タ����ʽ����2����ƽ����߅�ε����|(zh��)��֪�� ���ú�δ֪��
���ú�δ֪��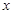 �Ĵ���(sh��)ʽ��ʾ
�Ĵ���(sh��)ʽ��ʾ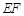 ���L�ȡ��t�ɵ��c
���L�ȡ��t�ɵ��c ���� ����3��ƽ����߅�������Č��Q�D�Σ��䌦�Q���Ğ�ɗl���Ǿ��Ľ��c����?q��)��Ǿ������c�����^���Q���ĵ�ֱ��ƽ��ƽ����߅�ε���e������^�c
���� ����3��ƽ����߅�������Č��Q�D�Σ��䌦�Q���Ğ�ɗl���Ǿ��Ľ��c����?q��)��Ǿ������c�����^���Q���ĵ�ֱ��ƽ��ƽ����߅�ε���e������^�c �c
�c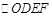 ���Q���ĵ�ֱ��ƽ��
���Q���ĵ�ֱ��ƽ��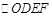 ����e����ô�ֱ��������Ҫ���
����e����ô�ֱ��������Ҫ���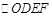 ���Q���ĵ�����.�t���c���˿ɴ_��ԓֱ��.
���Q���ĵ�����.�t���c���˿ɴ_��ԓֱ��.
ԇ�}������
��1��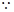 �c
�c
 ��
��
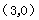 �ڒ��タ
�ڒ��タ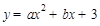 �ϣ�
�ϣ�
��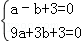 ��
��
���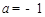 ��
��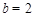 ��
��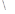 ���タ�Ľ���ʽ�飺
���タ�Ľ���ʽ�飺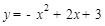 ��
��
��2���ڒ��タ����ʽ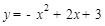 �У���
����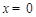 ����
����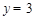 ��
��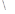

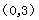 ��
��
�O(sh��)ֱ��BC�Ľ���ʽ��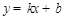 ����
����
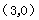 ��
��
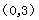 ���˴���ã�
���˴���ã�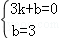 �����
�����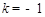 ��
��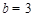 ����
����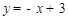 ��
��
�O(sh��)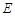 �c���˞�
�c���˞�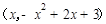 ���t
���t
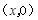 ��
��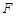
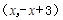 ��
��
��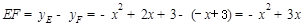
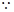 ��߅��
��߅��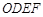 ��ƽ����߅�Σ�
��ƽ����߅�Σ�
�� ��
��
��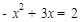 ����
����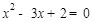 ��
��
���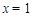 ��
��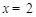 ��
��
�� �c���˞�
�c���˞�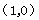 ��
��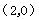 ��
��
��3��ƽ����߅�������Č��Q�D�Σ��䌦�Q���Ğ�ɗl���Ǿ��Ľ��c����?q��)��Ǿ������c�����^���Q���ĵ�ֱ��ƽ��ƽ����߅�ε���e������^�c �c
�c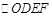 ���Q���ĵ�ֱ��ƽ��
���Q���ĵ�ֱ��ƽ��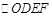 ����e��
����e��
�ٮ�
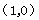 �r���c
�r���c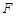 ���˞�
���˞�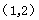 ����
����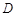
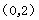
�O(sh��)���Ǿ� �����c��
�����c��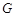 ���t
���t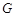
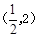 ��
��
�O(sh��)ֱ��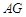 �Ľ���ʽ��
�Ľ���ʽ��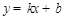 ����
����
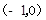 ��
��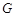
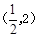 ���˴���ã�
���˴���ã�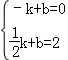 ��
��
���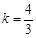 ��
�� 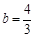 ��������ֱ���Ľ���ʽ�飺
��������ֱ���Ľ���ʽ�飺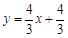


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D��ʾ��ֱ��l��y=3x+3�cx�S�����cA���cy�S�����cB���ѡ�AOB��y�S���ۣ��cA�䵽�cC�����タ�^�cB��C��D��3��0����
��1����ֱ��BD�͒��タ�Ľ���ʽ��
��2����BD�c���タ�Č��Q�S�����cM���cN�������S�ϣ����cN��B��D����c���������c��MCD���ƣ������НM��l�����cN�����ˣ�
��3���ڒ��タ���Ƿ�����cP��ʹS��PBD=6�������ڣ�����cP�����ˣ��������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪���κ���(sh��)�D�����c�ǣ�-1��2�������^�c��0�� ����
����
��1������κ���(sh��)�ı��_ʽ�����ڈD�Ю������ĈD��
��2���Д��c��2�� ���Ƿ���ԓ���κ���(sh��)�D���ϣ���ָ����
���Ƿ���ԓ���κ���(sh��)�D���ϣ���ָ���� ȡ��ֵ�r��
ȡ��ֵ�r��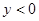 ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�����䌍����(w��)Ժ��ָʾ����ij�ط��������_��һϵ�С����r(n��ng)����(y��u)�����ߣ�ʹ�r(n��ng)�������������ӣ�ij�r(n��ng)�����a(ch��n)��(j��ng)�Nһ�N�r(n��ng)�a(ch��n)Ʒ����֪�@�N�a(ch��n)Ʒ�ijɱ��r��ÿǧ��20Ԫ���Ј��{(di��o)��l(f��)�F(xi��n)��ԓ�a(ch��n)Ʒÿ����N����y��ǧ�ˣ��c�N�ۃrx��Ԫ/ǧ�ˣ��������P(gu��n)ϵ��y=��2x+80���O(sh��)�@�N�a(ch��n)Ʒÿ����N��������wԪ��
��1����w�cx֮�g�ĺ���(sh��)�P(gu��n)ϵʽ��
��2��ԓ�a(ch��n)Ʒ�N�ۃr����ÿǧ�˶���Ԫ�r��ÿ����N�����������������Ƕ���Ԫ��
��3�������r���TҎ(gu��)���@�N�a(ch��n)Ʒ���N�ۃr������ÿǧ��28Ԫ��ԓ�r(n��ng)����Ҫÿ��@��150Ԫ���N���������N�ۃr��(y��ng)����ÿǧ�˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪���� �Ѓɂ���ͬ�Č���(sh��)��������
�Ѓɂ���ͬ�Č���(sh��)�������� Ҳ�Ѓɂ���ͬ�Č���(sh��)��������ɸ����ڷ���
Ҳ�Ѓɂ���ͬ�Č���(sh��)��������ɸ����ڷ��� �ăɸ�֮�g����k��ȡֵ������
�ăɸ�֮�g����k��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D�����タ ����c��Q���c
����c��Q���c �S����A(-1��0)��B(5�� 0)���c���c
�S����A(-1��0)��B(5�� 0)���c���c �S����C�c��
�S����C�c��
(1)ֱ�ӌ������タ�Ľ���ʽ������cQ�����ˣ�
(2)��ԓ���タ�Č��Q�S����һ�c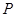 ,ʹ�á�
,ʹ�á� �����L��С.Ո�ڈD�Ю����c
�����L��С.Ո�ڈD�Ю����c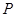 ��λ�ã������c
��λ�ã������c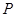 �����ˣ�
�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D�����タ �cֱ��
�cֱ�� �����cA ��B���cy�S�����cC��
�����cA ��B���cy�S�����cC��
��1�����cA��B�����ˣ�
��2�����cP��ֱ��x=1��һ�c���Ƿ���ڡ�PAB�ǵ��������Σ������ڣ�������з��ϗl�����cP�����ˣ��������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D��Ҫ�O(sh��)Ӌһ�����εĻ����������L60 m����40 m���Ѓɗl�v������һ�l�M�������M�����ăɂ�(c��)�Ѓɂ���A�h(hu��n)��������A�h(hu��n)�����ă�(n��i)��A�İ돽��10 m���M�����Č����������������ȵ�2�����O(sh��)�M�����Č���2x m�����е�ֵȡ3��
��1���ú�x��ʽ�ӱ�ʾ�ɂ���A�h(hu��n)��������e֮�ͣ�
��2��������������e֮�ͱȾ�����e�� ��36 m2�r����x��ֵ��
��36 m2�r����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D����֪���タ �ĈD���cx�S��һ�����c��B��5��0������һ�����c��A�����cy�S�����cC��0��5����
�ĈD���cx�S��һ�����c��B��5��0������һ�����c��A�����cy�S�����cC��0��5����
��1����ֱ��BC�c���タ�Ľ���ʽ��
��2�����cM�ǒ��タ��x�S�·��D���ϵĄ��c���^�cM��MN��y�S��ֱ��BC���cN����MN�����ֵ��
��3���ڣ�2���ėl���£�MNȡ�����ֵ�r�����cP�ǒ��タ��x�S�·��D��������һ�c����BC��߅��ƽ����߅��CBPQ���O(sh��)ƽ����߅��CBPQ����e��S1����ABN����e��S2����S1=6S2�����cP�����ˡ�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com