
(1)觀察發現
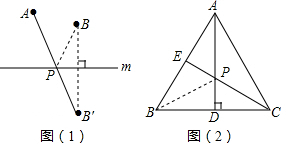
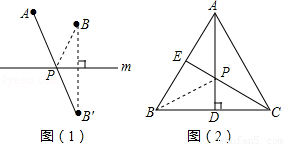
如圖(1):若點A、B在直線m同側,在直線m上找一點P,使AP+BP的值最小,做法如下:
作點B關于直線m的對稱點B′,連接AB′,與直線m的交點就是所求的點P,線段AB′的長度即為AP+BP的最小值.
如圖(2):在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小,做法如下:
作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 .
(2)實踐運用
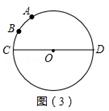
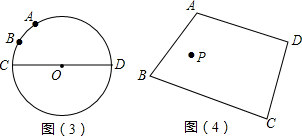
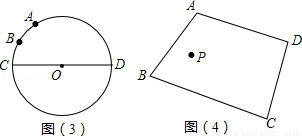
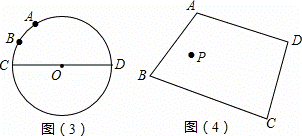
如圖(3):已知⊙O的直徑CD為2,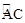 的度數為60°,點B是
的度數為60°,點B是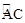 的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的值最小,則BP+AP的最小值為 .
的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的值最小,則BP+AP的最小值為 .
(3)拓展延伸
如圖(4):點P是四邊形ABCD內一點,分別在邊AB、BC上作出點M,點N,使PM+PN的值最小,保留作圖痕跡,不寫作法.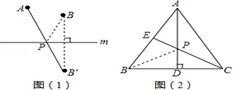

解:(1)=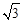 。
。
(2)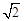 。
。
(3)拓展延伸:作圖如下: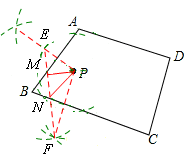
解析分析:(1)觀察發現:利用作法得到CE的長為BP+PE的最小值:
∵在等邊三角形ABC中,AB=2,點E是AB的中點
∴CE⊥AB,∠BCE=∠BCA=30°,BE=1。
∴CE=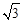 BE=
BE=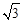 。
。
(2)實踐運用:過B點作弦BE⊥CD,連結AE交CD于P點,連結OB、OE、OA、PB,根據垂徑定理得到CD平分BE,即點E與點B關于CD對稱,則AE的長就是BP+AP的最小值:
∵BE⊥CD,∴CD平分BE,即點E與點B關于CD對稱。
∵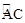 的度數為60°,點B是
的度數為60°,點B是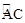 的中點,∴∠BOC=30°,∠AOC=60°。∴∠EOC=30°。
的中點,∴∠BOC=30°,∠AOC=60°。∴∠EOC=30°。
∴∠AOE=60°+30°=90°。
∵OA=OE=1,∴AE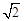 OA=
OA=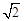 。
。
∵AE的長就是BP+AP的最小值,∴BP+AP的最小值是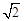 。
。
(3)拓展延伸:分別作出點P關于AB和BC的對稱點E和F,然后連接EF,EF交AB于M、交BC于N。則點M,點N,使PM+PN的值最小。
解:(1)觀察發現: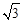 。
。
(2)實踐運用:
如圖,過B點作弦BE⊥CD,連接AE交CD于P點,連接OB、OE、OA、PB,則點P 即為使BP+AP的值最小的點。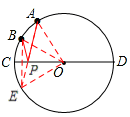
BP+AP的最小值是 。
。
(3)拓展延伸:作圖如下:


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案科目:初中數學 來源: 題型:
| 3 |
| 3 |
 |
| AC |
 |
| AC |
| 2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(貴州六盤水卷)數學(解析版) 題型:解答題
(1)觀察發現
如圖(1):若點A、B在直線m同側,在直線m上找一點P,使AP+BP的值最小,做法如下:
作點B關于直線m的對稱點B′,連接AB′,與直線m的交點就是所求的點P,線段AB′的長度即為AP+BP的最小值.
如圖(2):在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小,做法如下:
作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 .
(2)實踐運用
如圖(3):已知⊙O的直徑CD為2,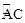 的度數為60°,點B是
的度數為60°,點B是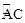 的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的值最小,則BP+AP的最小值為 .
的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的值最小,則BP+AP的最小值為 .
(3)拓展延伸
如圖(4):點P是四邊形ABCD內一點,分別在邊AB、BC上作出點M,點N,使PM+PN的值最小,保留作圖痕跡,不寫作法.
查看答案和解析>>
科目:初中數學 來源: 題型:
(1)觀察發現
如圖(1):若點A、B在直線m同側,在直線m上找一點P,使AP+BP的值最小,做法如下:
作點B關于直線m的對稱點B′,連接AB′,與直線m的交點就是所求的點P,線段AB′的長度即為AP+BP的最小值.
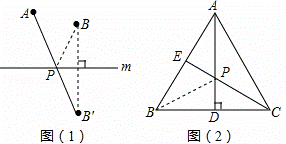
如圖(2):在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小,做法如下:
作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 ![]() .
.
(2)實踐運用
如圖(3):已知⊙O的直徑CD為2,![]() 的度數為60°,點B是
的度數為60°,點B是![]() 的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的值最小,則BP+AP的最小值為
的中點,在直徑CD上作出點P,使BP+AP的值最小,則BP+AP的值最小,則BP+AP的最小值為 ![]() .
.
(3)拓展延伸
如圖(4):點P是四邊形ABCD內一點,分別在邊AB、BC上作出點M,點N,使PM+PN的值最小,保留作圖痕跡,不寫作法.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com