
【題目】如圖,四邊形ABCD是邊長為1的正方形,E,F為BD所在直線上的兩點,若AE= ![]() ,∠EAF=135°,則下列結論正確的是( )
,∠EAF=135°,則下列結論正確的是( ) 
A.DE=1
B.tan∠AFO= ![]()
C.AF= ![]()
D.四邊形AFCE的面積為 ![]()
【答案】C
【解析】解:∵四邊形ABCD是正方形, ∴AB=CB=CD=AD=1,AC⊥BD,∠ADO=∠ABO=45°,
∴OD=OB=OA= ![]() ,∠ABF=∠ADE=135°,
,∠ABF=∠ADE=135°,
在Rt△AEO中,EO= ![]() =
= ![]() =
= ![]() ,
,
∴DE= ![]() ,故A錯誤.
,故A錯誤.
∵∠EAF=135°,∠BAD=90°,
∴∠BAF+∠DAE=45°,
∵∠ADO=∠DAE+∠AED=45°,
∴∠BAF=∠AED,
∴△ABF∽△EDA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BF= ![]() ,
,
在Rt△AOF中,AF= ![]() =
= ![]() =
= ![]() ,故C正確,
,故C正確,
tan∠AFO= ![]() =
= ![]() =
= ![]() ,故B錯誤,
,故B錯誤,
∴S四邊形AECF= ![]() ACEF=
ACEF= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,故D錯誤,
,故D錯誤,
故選C.
【考點精析】解答此題的關鍵在于理解正方形的性質的相關知識,掌握正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形,以及對解直角三角形的理解,了解解直角三角形的依據:①邊的關系a2+b2=c2;②角的關系:A+B=90°;③邊角關系:三角函數的定義.(注意:盡量避免使用中間數據和除法).


科目:初中數學 來源: 題型:
【題目】根據圖1的程序,得到了y與x的函數圖象,如圖2,若點M是y軸正半軸上任意一點,過點M作PQ∥x軸交圖象于點P,Q,連接OP,OQ,則下列結論:①x<0時,y= ![]() ;②△OPQ的面積為定值;③x>0時,y隨x的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正確的有( )
;②△OPQ的面積為定值;③x>0時,y隨x的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正確的有( )
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,拋物線y=ax2﹣5ax+4a與x軸交于A、B(A點在B點的左側)與y軸交于點C.
(1)如圖1,連接AC、BC,若△ABC的面積為3時,求拋物線的解析式;
(2)如圖2,點P為第四象限拋物線上一點,連接PC,若∠BCP=2∠ABC時,求點P的橫坐標;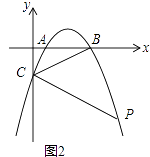
(3)如圖3,在(2)的條件下,點F在AP上,過點P作PH⊥x軸于H點,點K在PH的延長線上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,連接KB并延長交拋物線于點Q,求PQ的長.
a,連接KB并延長交拋物線于點Q,求PQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店購買一批單價為20元的日用品,如果以單價30元銷售,那么半月內可以售出400件.據銷售經驗,提高銷售單價會導致銷售量的減少,即銷售單價每提高一元,銷售量相應減少20件.如何提高銷售價,才能在半月內獲得最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明隨機調查了若干市民租用共享單車的騎車時間t(單位:分),將獲得的數據分成四組,繪制了如下統計圖(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根據圖中信息,解答下列問題: 
(1)這項被調查的總人數是多少人?
(2)試求表示A組的扇形統計圖的圓心角的度數,補全條形統計圖;
(3)如果小明想從D組的甲、乙、丙、丁四人中隨機選擇兩人了解平時租用共享單車情況,請用列表或畫樹狀圖的方法求出恰好選中甲的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國魏晉時期數學家劉徽首創“割圓術”計算圓周率.隨著時代發展,現在人們依據頻率估計概率這一原理,常用隨機模擬的方法對圓周率π進行估計,用計算機隨機產生m個有序數對(x,y)(x,y是實數,且0≤x≤1,0≤y≤1),它們對應的點在平面直角坐標系中全部在某一個正方形的邊界及其內部.如果統計出這些點中到原點的距離小于或等于1的點有n個,則據此可估計π的值為 . (用含m,n的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y= ![]() (k為常數).
(k為常數).
(1)若點P1( ![]() ,y1)和點P2(﹣
,y1)和點P2(﹣ ![]() ,y2)是該反比例函數圖象上的兩點,試利用反比例函數的性質比較y1和y2的大小;
,y2)是該反比例函數圖象上的兩點,試利用反比例函數的性質比較y1和y2的大小;
(2)設點P(m,n)(m>0)是其圖象上的一點,過點P作PM⊥x軸于點M.若tan∠POM=2,PO= ![]() (O為坐標原點),求k的值,并直接寫出不等式kx+
(O為坐標原點),求k的值,并直接寫出不等式kx+ ![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解答題
(1)如圖1,在正方形ABCD中,點E,F分別在BC,CD上,AE⊥BF于點M,求證:AE=BF; 
(2)如圖2,將 (1)中的正方形ABCD改為矩形ABCD,AB=2,BC=3,AE⊥BF于點M,探究AE與BF的數量關系,并證明你的結論. 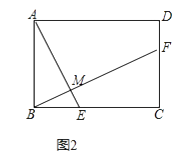
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com