
 ,
, )的切線交x軸于A點,交y軸于B點.
)的切線交x軸于A點,交y軸于B點.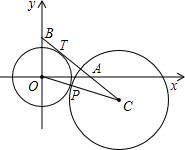 為(x,y),問N點的坐標x,y能否寫成與r無關的關系式?若能,請寫出關系式;若不能,請說明理由.
為(x,y),問N點的坐標x,y能否寫成與r無關的關系式?若能,請寫出關系式;若不能,請說明理由.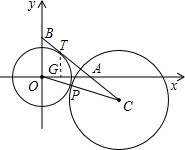 (1)解:過T作TG⊥x軸于G;
(1)解:過T作TG⊥x軸于G;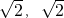 ),
), ,
,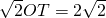 .
.
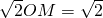 (2+r),
(2+r),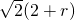 ①,
①, y,
y, y;
y; y]2=(2+r)2②;
y]2=(2+r)2②;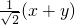 ,代入②得:4+[
,代入②得:4+[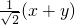 -
- ]2=(
]2=(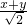 )2,
)2, .
. ,由此可求得OA、OB的長.
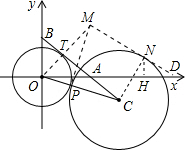
,由此可求得OA、OB的長. OM,OM等于兩圓的半徑和,聯立上述兩式可得x、y、r的第一個關系式;易求得MN的長,即TC的長,可在Rt△OTC中,根據勾股定理得到另外一個x、y、r的關系式,聯立兩式即可得到x、y的關系式.
OM,OM等于兩圓的半徑和,聯立上述兩式可得x、y、r的第一個關系式;易求得MN的長,即TC的長,可在Rt△OTC中,根據勾股定理得到另外一個x、y、r的關系式,聯立兩式即可得到x、y的關系式.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 結果保留根號)
結果保留根號)查看答案和解析>>
科目:初中數學 來源: 題型:
| 2 |
| 2 |
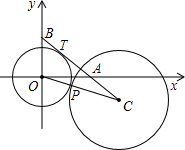 為(x,y),問N點的坐標x,y能否寫成與r無關的關系式?若能,請寫出關系式;若不能,請說明理由.
為(x,y),問N點的坐標x,y能否寫成與r無關的關系式?若能,請寫出關系式;若不能,請說明理由.查看答案和解析>>
科目:初中數學 來源:2013-2014學年廣東汕頭友聯中學九年級上學期第二次階段測試數學試卷(解析版) 題型:解答題
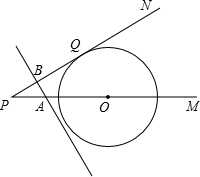
如圖,已知⊙O的圓心O在射線PM上,PN切⊙O于Q,PO=20cm,∠P=30°,A、B兩點同時從P點出發,點A沿PN方向移動,點B以4cm/s的速度沿PM方向移動,且直線AB始終垂直PN.設運動時間為t秒,求下列問題.(結果保留根號)

(1)求PQ的長
(2)當t為何值時直線AB與⊙o相切?
查看答案和解析>>
科目:初中數學 來源:2010年重慶市巫山縣中考數學模擬試卷(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2002年湖北省黃石市中考數學試卷(解析版) 題型:解答題
 ,
, )的切線交x軸于A點,交y軸于B點.
)的切線交x軸于A點,交y軸于B點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com