

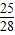 x2-
x2- x+7.
x+7. x2-
x2-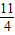 x+7.
x+7.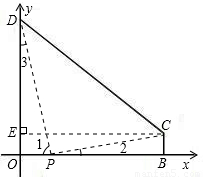 解:(1)過點C作CE⊥OD于點E,則四邊形OBCE為矩形.
解:(1)過點C作CE⊥OD于點E,則四邊形OBCE為矩形.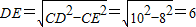 .
.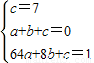 ,
, ,
,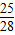 x2-
x2-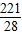 x+7.(9分)
x+7.(9分)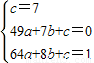 ,
,
 x2-
x2-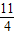 x+7.(10分)
x+7.(10分)

科目:初中數學 來源:2007年全國中考數學試題匯編《二次函數》(06)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2010年中考數學模擬試卷冀教版(解析版) 題型:選擇題

查看答案和解析>>
科目:初中數學 來源:2009年湖南省邵陽市邵東縣中考保送生考試數學試卷(解析版) 題型:選擇題
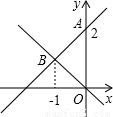
查看答案和解析>>
科目:初中數學 來源:2007年陜西省中考數學試卷(大綱卷)(解析版) 題型:選擇題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com