
【題目】一個不透明的口袋中裝有4個完全相同的小球,分別標有數字1、2、3、4,另有一個可以自由旋轉的圓盤.被分成面積相等的3個扇形區,分別標有數字1、2、3(如圖所示).小穎和小亮想通過游戲來決定誰代表學校參加歌詠比賽,游戲規則為:一人從口袋中摸出一個小球,另一個人轉動圓盤,如果所摸球上的數字與圓盤上轉出數字之和小于4,那么小穎去;否則小亮去.
(1)用樹狀圖或列表法求出小穎參加比賽的概率;
(2)你認為該游戲公平嗎?請說明理由;若不公平,請修改該游戲規則,使游戲公平.

【答案】(1)小穎參加比賽的概率為:![]() ;(2)游戲不公平;可改為:若兩個數字之和小于5,則小穎去參賽;否則,小亮去參賽.
;(2)游戲不公平;可改為:若兩個數字之和小于5,則小穎去參賽;否則,小亮去參賽.
【解析】
試題分析:(1)首先根據題意畫出樹狀圖,由樹狀圖求得所有等可能的結果與兩指針所指數字之和和小于4的情況,則可求得小穎參加比賽的概率;
(2)根據小穎獲勝與小亮獲勝的概率,比較概率是否相等,即可判定游戲是否公平;使游戲公平,只要概率相等即可.
解:(1)畫樹狀圖得:
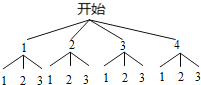
∵共有12種等可能的結果,所指數字之和小于4的有3種情況,
∴P(和小于4)=![]() =
=![]() ,
,
∴小穎參加比賽的概率為:![]() ;
;
(2)不公平,
∵P(小穎)=![]() ,
,
P(小亮)=![]() .
.
∴P(和小于4)≠P(和大于等于4),
∴游戲不公平;
可改為:若兩個數字之和小于5,則小穎去參賽;否則,小亮去參賽.


 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:
【題目】直線MN與直線PQ垂直相交于O,點A在直線PQ上運動,點B在直線MN上運動.
(1)如圖1,已知AE、BE分別是∠BAO和∠ABO角的平分線,點A、B在運動的過程中,∠AEB的大小是否會發生變化?若發生變化,請說明變化的情況;若不發生變化,試求出∠AEB的大小.
(2)如圖2,已知AB不平行CD,AD、BC分別是∠BAP和∠ABM的角平分線,又DE、CE分別是∠ADC和∠BCD的角平分線,點A、B在運動的過程中,∠CED的大小是否會發生變化?若發生變化,請說明理由;若不發生變化,試求出其值.
(3)如圖3,延長BA至G,已知∠BAO、∠OAG的角平分線與∠BOQ的角平分線及延長線相交于E、F,在△AEF中,如果有一個角是另一個角的3倍,試求∠ABO的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD,AD∥BC,∠B=90,AD=6,AB=4,BC=9.

(1)求CD的長為.
(2)點P從點B出發,以每秒1個單位的速度沿著邊BC向點C運動,連接DP.設點P運動的時間為t秒,則當t為何值時,△PDC為等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
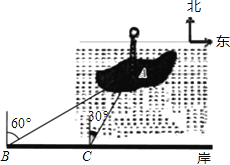
【題目】如圖,郴州北湖公園的小島上有為了紀念唐代著名詩人韓愈而建的韓愈銅像,其底部為A,某人在岸邊的B處測得A在B的北偏東60°的方向上,然后沿岸邊直行200米到達C處,再次測得A在C的北偏東30°的方向上(其中A,B,C在同一平面上).求這個銅像底部A到岸邊BC的距離(結果精確到0.1米,參考數據:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,BE⊥AC于E,且D、E分別是AB、AC的中點.延長BC至點F,使CF=CE.

(1)求∠ABC的度數;
(2)求證:BE=FE;
(3)若AB=2,求△CEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣x+m=0有兩個不相等的實數根.
(1)求實數m的取值范圍;
(2)若方程的兩個實數根為x1、x2,且x1+x2+x1x2=m2﹣1,求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com