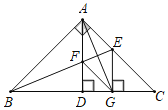
【題目】如圖，等腰Rt△ABC中，∠BAC＝90°，AD⊥BC于點D，∠ABC的平分線分別交AC、AD于E、F兩點，EG⊥BC于點G，連接AG、FG．下列結論：①AE＝CE；②△ABF≌△GBF；③BE⊥AG；④△AEF為等腰三角形．其中正確結論的個數是（ ）
A.1個B.2個C.3個D.4個
【答案】C
【解析】
利用全等三角形的性質以及角平分線的性質定理一一判斷即可．
∵BF平分∠ABC，∠BAC＝90°，EG⊥BC
∴AE＝EG，
∵EC＞EG，
∴EC＞AE，故①錯誤，
∵AE＝EG，BE＝BE
∴Rt△ABE≌Rt△GBE（HL）
∴AB＝BG，
∴點B在AG的垂直平分線上，
∵AE＝EG
∴點E在AG的垂直平分線上
∴BE是AG的垂直平分線
∴BE⊥AG，故③正確，
∵BA＝BG，∠ABF＝∠GBF，BF＝BF，
∴△ABF≌△GBF（SAS），故②正確，
∵BE是AG的垂直平分線
∴AF＝FG，EF⊥AG
∴∠AFE＝∠EFG
∵AD⊥BC，EG⊥BC
∴AD∥EG
∴∠AFE＝∠FEG
∴∠EFG＝∠FEG
∴FG＝EG
∴AF＝FG＝EG＝AE，故④正確，
故選：C．
開心快樂假期作業暑假作業西安出版社系列答案
名題訓練系列答案科目：初中數學 來源： 題型：
【題目】某水果店老板用400元購進一批葡萄，由于葡萄新鮮很快售完，老板又用500元購進第二批葡萄，所購數量與第一批相同，但每千克進價比第一批貴2元.
（1）求第一批葡萄進價為每千克多少元；
（2）若老板以每千克11元的價格將兩批葡萄全部售完，可以盈利多少元.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
①經過三個點一定可以作圓；②若等腰三角形的兩邊長分別為3和7，則第三邊長是3或7；③一個正六邊形的內角和是其外角和的2倍；④隨意翻到一本書的某頁，頁碼是偶數是隨機事件；⑤關于x的一元二次方程x2-(k+3)x+k=0有兩個不相等的實數根．
A.①②③B.①④⑤C.②③④D.③④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖1，O是等邊△ABC內一點，連接OA、OB、OC，且OA=3，OB=4，OC=5，將△BAO繞點B順時針旋轉后得到△BCD，連接OD．求：
①旋轉角的度數；
②線段OD的長；
③∠BDC的度數．
（2）如圖2所示，O是等腰直角△ABC（∠ABC=90°）內一點，連接OA、OB、OC，將△BAO繞點B順時針旋轉后得到△BCD，連接OD．當OA、OB、OC滿足什么條件時，∠ODC=90°？請給出證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程tx26x+m+4=0有兩個實數根x1、x2．
（1）當m=1時，求t的取值范圍；
（2）當t=1時，若x1、x2滿足3| x1|=x2+4，求m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了加強課外閱讀，開闊視野，我校開展了“書香校園”的主題活動.學校隨機抽取了部分學生，對他們一周的課外閱讀時間進行調查，繪制成如下頻數分布表和不完整的頻數直方
圖：
請根據圖表信息回答下列問題：
（1）頻數分布表中的a=_______，b=_______；
（2）將頻數直方圖補充完整；
（3）全校共有學生1200人，若規定閱讀時間超過2小時則評為“優秀閱讀員”，請估計能評為“優秀閱讀員”的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，⊙ P的圓心坐標是(2，a)(a>2)，半徑為2，函數y＝x的圖象被⊙ P截得的弦AB的長為
，則a的值是 ( )
A. 
B. 
C. D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
