Question

如圖，△ABC中，AB=BC，AC=8，tanA=k，P為AC邊上一動點，設PC=x，作PE∥AB交BC于E，PF∥BC交AB于F．

（1）證明：△PCE是等腰三角形；

（2）EM、FN、BH分別是△PEC、△AFP、△ABC的高，用含x和k的代數式表示EM、FN，并探究EM、FN、BH之間的數量關系；

（3）當k=4時，求四邊形PEBF的面積S與x的函數關系式．x為何值時，S有最大值？并求出S的最大值．

 

Answer 1

【答案】

解：（1）證明：∵AB=BC，∴∠A=∠C。

∵PE∥AB，∴∠CPE=∠A。

∴∠CPE=∠C。∴△PCE是等腰三角形。

（2）∵△PCE是等腰三角形，EM⊥CP，∴CM=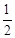CP=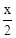，tanC=tanA=k。

∴EM=CM•tanC=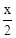•k=。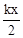

同理：FN=AN•tanA=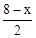•k=4k﹣。

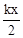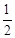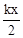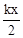由于BH=AH•tanA=×8•k=4k，EM+FN=+4k﹣=4k，

∴EM+FN=BH。

（3）當k=4時，EM=2x，FN=16﹣2x，BH=16，

∴S_△PCE=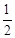x•2x=x²，S_△APF=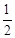（8﹣x）•（16﹣2x）=（8﹣x）²，S_△ABC=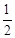×8×16=64。

∴。

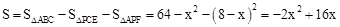∴當k=4時，四邊形PEBF的面積S與x的函數關系式為。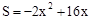

∵，

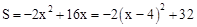∴當x=4時，S有最大值32。

【解析】（1）根據等邊對等角可得∠A=∠C，然后根據兩直線平行，同位角相等求出∠CPE=∠A，從而得到∠CPE=∠C，即可得證。

（2）根據等腰三角形三線合一的性質求出CM=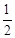CP，然后求出EM，同理求出FN、BH的長，再根據結果整理可得EM+FN=BH。

（3）分別求出EM、FN、BH，然后根據S_△PCE，S_△APF，S_△ABC，再根據，整理即可得到S與x的關系式，然后利用二次函數的最值問題解答。