
 利用三角形內角和,探究四邊形內角和:
利用三角形內角和,探究四邊形內角和:
 (∠ABC+∠BCD)=
(∠ABC+∠BCD)= ×140°=70°,
×140°=70°, (∠ABC+∠BCD)的度數,然后利用三角形的內角和定理列式即可求出∠BEC的度數.
(∠ABC+∠BCD)的度數,然后利用三角形的內角和定理列式即可求出∠BEC的度數.

科目:初中數學 來源: 題型:
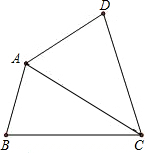 利用三角形內角和,探究四邊形內角和:
利用三角形內角和,探究四邊形內角和: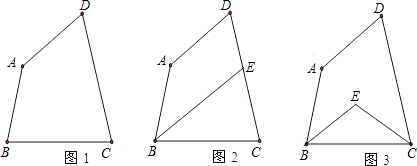
查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(福建漳州卷)數學(解析版) 題型:解答題
(1)問題探究
數學課上,李老師給出以下命題,要求加以證明.
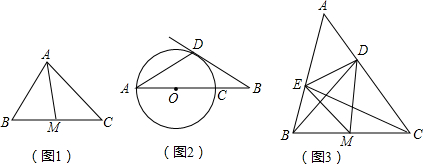
如圖1,在△ABC中,M為BC的中點,且MA= BC,求證∠BAC=90°.
BC,求證∠BAC=90°.
同學們經過思考、討論、交流,得到以下證明思路:
思路一 直接利用等腰三角形性質和三角形內角和定理…
思路二 延長AM到D使DM=MA,連接DB,DC,利用矩形的知識…
思路三 以BC為直徑作圓,利用圓的知識…
思路四…
請選擇一種方法寫出完整的證明過程;
(2)結論應用
李老師要求同學們很好地理解(1)中命題的條件和結論,并直接運用(1)命題的結論完成以下兩道題:
①如圖2,線段AB經過圓心O,交⊙O于點A,C,點D在⊙O上,且∠DAB=30°,OA=a,OB=2a,求證:直線BD是⊙O的切線;
②如圖3,△ABC中,M為BC的中點,BD⊥AC于D,E在AB邊上,且EM=DM,連接DE,CE,如果∠A=60°,請求出△ADE與△ABC面積的比值.

查看答案和解析>>
科目:初中數學 來源:2013年福建省漳州市中考數學試卷 (解析版) 題型:解答題
 BC,求證∠BAC=90°.
BC,求證∠BAC=90°.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com