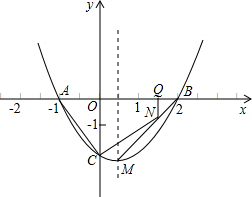
解:(1)設拋物線的解析式y=a(x+1)(x-2),
∵-2=a×1×(-2),
∴a=1,
∴y=x
2-x-2,其頂點坐標是(

,-

);
(2)設線段BM所在的直線的解析式為:y=kx+b,點N的坐標為N(h,-t),
則
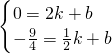
,
解它們組成的方程組得:

,
所以線段BM所在的直線的解析式為:y=

x-3,
N點縱坐標為:-t,
∴-t=

h-3,
∴h=2-

t,
其中

<h<2,
∴s=
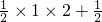
(2+t)(2-

t)=-

t
2+

t+3,
∴s與t間的函數解析式為,
s=-

t
2+

t+3,
∵M點坐標是(

,-

);
∴QN最大值為:

,
∴自變量的取值圍是:
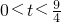
;
(3)存在符合條件的點P,且坐標是:P
1(

,

),P
2(
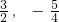
).
設點P的坐標為P(m,n),則 n=m
2-m-2,PA
2=(m+1)
2+n
2PC
2=m
2+(n+2)
2,AC
2=5,
分以下幾種情況討論:
(ⅰ)若∠APC=90°則AC
2=PC
2+AP
2.
可得:m
2+(n+2)
2+(m+1)
2+n
2=5,
解得:
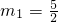
,m
2=-1(舍去).
所以點P(

,

)
(ⅱ)若∠PAC=90°,則PC
2=PA
2+AC
2∴n=m
2-m-2
(m+1)
2+n
2=m
2+(n+2)
2+5
解得:
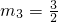
,m
4=0(舍去).所以點P(

,-

).
(ⅲ)由圖象觀察得,當點P在對稱軸右側時,PA>AC,所以邊AC的對角∠APC不可能是直角.
(4)以點O,點A(或點O,點C)為矩形的兩個頂點,第三個頂點落在矩形這一邊OA(或邊OC)的對邊上,
如圖,此時未知頂點坐標是點P(-1,-2),以點A,點C為矩形的兩頂點,
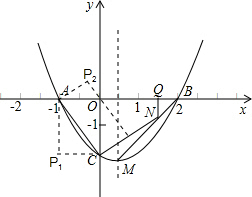
第三個頂點落在矩形這一邊AC的對邊上,
如圖,此時未知頂點坐標是P
1(-1,-2),P
2(-
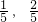
)或
(

,-

).
分析:(1)利用交點式可以求出二次函數解析式,再利用公式法求出頂點坐標,
(2)運用兩點求出直線BM解析式,再表示出四邊形面積,
(3)根據使△PAC為直角三角形,三個角依次分析當等于直角時,得出不同結論.
(4)作出矩形,利用勾股定理可以求出.
點評:此題主要考查了二次函數解析式的求法,以及頂點坐標計算,四邊形面積計算,矩形的性質等,綜合性比較強.

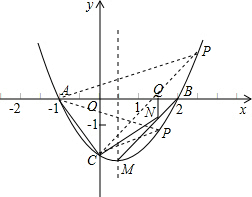
 已知二次函數的圖象如圖所示.
已知二次函數的圖象如圖所示. 解:(1)設拋物線的解析式y=a(x+1)(x-2),
解:(1)設拋物線的解析式y=a(x+1)(x-2), ,-
,- );
);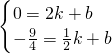 ,
, ,
, x-3,
x-3, h-3,
h-3, t,
t, <h<2,
<h<2,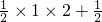 (2+t)(2-
(2+t)(2- t)=-
t)=- t2+
t2+ t+3,
t+3, t2+
t2+ t+3,
t+3, ,-
,- );
); ,
,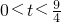 ;
; ,
, ),P2(
),P2(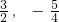 ).
).
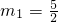 ,m2=-1(舍去).
,m2=-1(舍去). ,
, )
)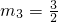 ,m4=0(舍去).所以點P(
,m4=0(舍去).所以點P( ,-
,- ).
).
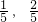 )或
)或 ,-
,- ).
).

 已知二次函數的圖象如右圖,則下列結論中,正確的結論有( )
已知二次函數的圖象如右圖,則下列結論中,正確的結論有( ) 已知二次函數的圖象如圖所示,
已知二次函數的圖象如圖所示,