
【題目】A、B兩地相距50km,甲于某日騎自行車從A地出發(fā)駛往B地,乙也于同日下午騎摩托車從A地出發(fā)駛往B地,在這個變化過程中,甲和乙所行駛的路程用變量s(km)表示,甲所用的時間用變量t(時)表示,圖中折線OPQ和線段MN分別表示甲和乙所行駛的路程s與時間t的變化關(guān)系,請根據(jù)圖象回答:

(1)直接寫出:甲出發(fā)后______小時,乙才開始出發(fā);
(2)請分別求出甲出發(fā)1小時后的速度和乙的行駛速度?
(3)求乙行駛幾小時后追上甲,此時兩人距B地還有多少千米?
【答案】(1)1;(2)甲:25km/h,乙:10km/h;(3)乙行駛![]() 小時后追上甲,此時兩人距
小時后追上甲,此時兩人距![]() 地還有
地還有![]() 千米
千米
【解析】
(1)觀察函數(shù)圖象得到甲出發(fā)后1小時,乙才開始出發(fā);
(2)根據(jù)路程除以時間等于速度,列式求解即可得到答案;
(3)設(shè)乙行駛![]() 小時后追上甲,根據(jù)題意得
小時后追上甲,根據(jù)題意得![]() ,求解即可得到答案;
,求解即可得到答案;
解:(1)觀察函數(shù)圖象得到甲出發(fā)后1小時,乙才開始出發(fā),
故填:1;
(2)由圖像信息可知:乙的速度為:![]() 千米/時,
千米/時,
甲出發(fā)1小時后的速度為:![]() 千米/時.
千米/時.
(3)設(shè)乙行駛![]() 小時后追上甲,結(jié)合圖片信息和(2)的結(jié)果得到:
小時后追上甲,結(jié)合圖片信息和(2)的結(jié)果得到:
![]() ,
,
解得![]() ,
,
即乙行駛![]() 小時后追上甲,此時兩人距
小時后追上甲,此時兩人距![]() 地還有
地還有![]() (千米);
(千米);
答:乙行駛![]() 小時后追上甲,此時兩人距
小時后追上甲,此時兩人距![]() 地還有
地還有![]() 千米;
千米;


科目:初中數(shù)學 來源: 題型:
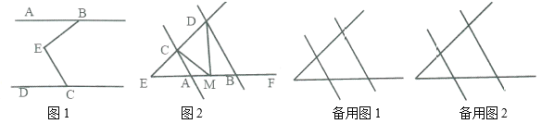
【題目】操作探究:
(1)實踐:如圖1, ![]() 中,
中,![]() 為
為![]() 邊上的中線,
邊上的中線,![]() 的面積記為
的面積記為![]() ,
,![]() 的面積記為
的面積記為![]() .則
.則![]() .
.

(2)探究:在圖2中,![]() 、
、![]() 分別為四邊形
分別為四邊形![]() 的邊
的邊![]() 、
、![]() 的中點,四邊形
的中點,四邊形![]() 的面積記為
的面積記為![]() ,陰影部分面積記為
,陰影部分面積記為![]() ,則
,則![]() 和
和![]() 之間滿足的關(guān)系式為______:
之間滿足的關(guān)系式為______:
(3)解決問題:
在圖3中,![]() 、
、![]() 、
、![]() 、
、![]() 分別為任意四邊形
分別為任意四邊形![]() 的邊
的邊![]() 、
、![]() 、
、![]() 、
、![]() 的中點,并且圖中陰影部分的面積為
的中點,并且圖中陰影部分的面積為![]() 平方厘米,求圖中四個小三角形的面積和,并說明理由.
平方厘米,求圖中四個小三角形的面積和,并說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某種事物經(jīng)歷了加熱,冷卻兩個聯(lián)系過程,折線圖DEF表示食物的溫度y(℃)與時間x(s)之間的函數(shù)關(guān)系(0≤x≤160),已知線段EF表示的函數(shù)關(guān)系中,時間每增加1s,食物溫度下降0.3℃,根據(jù)圖象解答下列問題;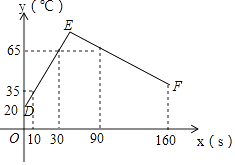
(1)當時間為20s、100s時,該食物的溫度分別為℃,℃;
(2)求線段DE所表示的y與x之間的函數(shù)表達式;
(3)時間是多少時,該食物的溫度最高?最高是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:如圖,在菱形ABCD中,對角線AC、BD相交于點O,DE∥AC,AE∥BD.
(1)、求證:四邊形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四邊形AODE的面積.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC,△CDE均為等邊三角形(每個內(nèi)角都是60°),連接BD,AE交于點O,BC與AE交于點P.試說明:∠POB=60°.經(jīng)過觀察分析,解題的關(guān)鍵是先利用( )說明△EAC≌△DBC.

A.SSSB.ASAC.SASD.AAS
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知![]() ,點
,點![]() 為平面內(nèi)一點.
為平面內(nèi)一點.
(1)如圖1,![]() 和
和![]() 互余,小明說過
互余,小明說過![]() 作
作![]() ,很容易說明
,很容易說明![]() 。請幫小明寫出具體過程;
。請幫小明寫出具體過程;
(2)如圖2,![]() ,當點
,當點![]() 在線段
在線段![]() 上移動時(點
上移動時(點![]() 與
與![]() ,
,![]() 兩點不重合),指出
兩點不重合),指出![]() 與
與![]() ,
,![]() 的數(shù)量關(guān)系?請說明理由;
的數(shù)量關(guān)系?請說明理由;
(3)在(2)的條件下,若點![]() 在
在![]() ,
,![]() 兩點外側(cè)運動(點
兩點外側(cè)運動(點![]() 與
與![]() ,
,![]() ,
,![]() 三點不重合)請直接寫出
三點不重合)請直接寫出![]() 與
與![]() ,
,![]() 的數(shù)量關(guān)系.
的數(shù)量關(guān)系.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某中學初三(1)班共有40名同學,在一次30秒跳繩測試中他們的成績統(tǒng)計如下表:
跳繩數(shù)/個 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 數(shù) | 1 | 2 | 8 | 11 | 5 |
將這些數(shù)據(jù)按組距5(個)分組,繪制成如圖的頻數(shù)分布直方圖(不完整).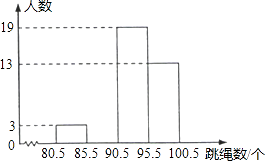
(1)將表中空缺的數(shù)據(jù)填寫完整,并補全頻數(shù)分布直方圖;
(2)這個班同學這次跳繩成績的眾數(shù)是個,中位數(shù)是個;
(3)若跳滿90個可得滿分,學校初三年級共有720人,試估計該中學初三年級還有多少人跳繩不能得滿分.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知:Rt△ABC中,∠C=90°,AC=BC=2,將一塊三角尺的直角頂點與斜邊AB的中點M重合,當三角尺繞著點M旋轉(zhuǎn)時,兩直角邊始終保持分別與邊BC、AC交于D,E兩點(D、E不與B、A重合).
(1)求證:MD=ME;
(2)求四邊形MDCE的面積;

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A,B的坐標分別為A(1,0)、B(3,0).拋物線y=x2﹣2mx+m2﹣4的頂點為P,與y軸的交點為Q.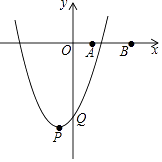
(1)填空:點P的坐標為;點Q的坐標為(均用含m的代數(shù)式表示)
(2)當拋物線經(jīng)過點A時,求點Q的坐標.
(3)連接QA、QB,設(shè)△QAB的面積為S,當拋物線與線段AB有公共點時,求S與m之間的函數(shù)關(guān)系式.
(4)點P、Q不重合時,以PQ為邊作正方形PQMN(P、Q、M、N分別按順時針方向排列).當正方形PQMN的四個頂點中,位于x軸兩側(cè)或y軸兩側(cè)的頂點個數(shù)相同時,直接寫出此時m的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com