Question

如圖，在等腰Rt△ABC中，P是斜邊BC的中點(diǎn)，以P為頂點(diǎn)的直角的兩邊分別與邊AB，AC交于點(diǎn)E，F(xiàn)，連接EF，當(dāng)∠EPF繞頂點(diǎn)P旋轉(zhuǎn)時(shí)（點(diǎn)E不與A，B重合），△PEF也始終是等腰直角三角形，請(qǐng)你說(shuō)明理由。

Answer 1

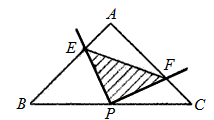
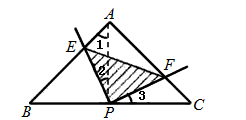
解：理由如下：連接PA， ∵PA是等腰△ABC底邊上的中線(xiàn)， ∴PA⊥PC（等腰三角形頂角的平分線(xiàn)、底邊上的中線(xiàn)、底邊上的高互相重合（三線(xiàn)合一））， 又AB⊥AC， ∴∠1=90°-∠PAC，∠C=90°-∠PAC， ∴∠1=∠C（等量代換）， 同理，由PA⊥PC，PE⊥PF可得∠2=∠3， 由PA是Rt△ABC斜邊上的中線(xiàn)，得：PA=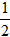BC=PC（直角三角形斜邊上的中線(xiàn)等于斜邊的一半）， 在△PAE和△PCF中，∠1=∠C，PA=PC，∠2=∠3， ∴△PAE≌△PCF（ASA）， ∴PE=PF（全等三角形對(duì)應(yīng)邊相等），因此，△PEF始終是等腰直角三角形。