
【題目】從﹣3,﹣1,1,3這五個(gè)數(shù)中,隨機(jī)抽取一個(gè)數(shù),記為a,若數(shù)a使關(guān)于x的不等式組 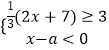 無解,且使關(guān)于x的分式方程
無解,且使關(guān)于x的分式方程 ![]() =﹣1有整數(shù)解,那么這5個(gè)數(shù)中所有滿足條件的a的值之和是( )
=﹣1有整數(shù)解,那么這5個(gè)數(shù)中所有滿足條件的a的值之和是( )
A.﹣2
B.﹣3
C.- ![]()
D.![]()
【答案】A
【解析】解:不等式組整理得: ![]() , 由不等式組無解,得到a≤1,即a=﹣3,﹣1,1,
, 由不等式組無解,得到a≤1,即a=﹣3,﹣1,1,
當(dāng)a=﹣3時(shí),分式方程為 ![]() ﹣
﹣ ![]() =﹣1,
=﹣1,
去分母得:x﹣5=﹣x+3,
解得:x=4,
經(jīng)檢驗(yàn)x=4是分式方程的解,且為整數(shù)解,滿足題意;
當(dāng)a=﹣1時(shí),分式方程為 ![]() ﹣
﹣ ![]() =﹣1,
=﹣1,
去分母得:x﹣3=﹣x+3,
解得:x=3,
經(jīng)檢驗(yàn)x=3是增根,分式方程無解,不滿足題意;
當(dāng)a=1時(shí),分式方程為 ![]() ﹣
﹣ ![]() =﹣1,
=﹣1,
去分母得:x﹣1=﹣x+3,
解得:x=2,
經(jīng)檢驗(yàn)x=2是分式方程的解,且為整數(shù)解,滿足題意,
則這5個(gè)數(shù)中所有滿足條件的a的值之和為﹣3+1=﹣2,
故選A
表示出不等式組中兩不等式的解集,由不等式組無解確定出a的值,代入分式方程判斷,求出滿足條件a的值,求出之和即可.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,菱形ABCD的頂點(diǎn)A的坐標(biāo)為![]() ,點(diǎn)B的坐標(biāo)為
,點(diǎn)B的坐標(biāo)為![]() ,點(diǎn)C在第一象限,對(duì)角線BD與x軸平行
,點(diǎn)C在第一象限,對(duì)角線BD與x軸平行![]() 直線
直線![]() 與x軸、y軸分別交于點(diǎn)E,
與x軸、y軸分別交于點(diǎn)E,![]() 將菱形ABCD沿x軸向左平移m個(gè)單位,當(dāng)點(diǎn)D落在
將菱形ABCD沿x軸向左平移m個(gè)單位,當(dāng)點(diǎn)D落在![]() 的內(nèi)部時(shí)
的內(nèi)部時(shí)![]() 不包括三角形的邊
不包括三角形的邊![]() ,m的值可能是
,m的值可能是![]()
![]()
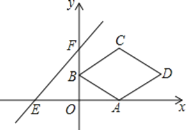
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在梯形ABCD中,AD∥BC,延長(zhǎng)CB到點(diǎn)E,使BE=AD,連接DE交AB于點(diǎn)M. 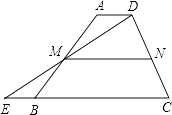
(1)求證:△AMD≌△BME;
(2)若N是CD的中點(diǎn),且MN=5,BE=2,求BC的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】四邊形ABCD中,對(duì)角線AC,BD相交于點(diǎn)O,給出下列四個(gè)條件:![]() ;
;![]() ;
;![]() ;
;![]() ,從中任選兩個(gè)條件,能使四邊形ABCD為平行四邊形的選法有
,從中任選兩個(gè)條件,能使四邊形ABCD為平行四邊形的選法有![]()
![]()
A. 2種 B. 3種 C. 4種 D. 5種
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:我們把對(duì)角線相等的四邊形叫做和美四邊形.
![]() 請(qǐng)舉出一種你所學(xué)過的特殊四邊形中是和美四邊形的例子.
請(qǐng)舉出一種你所學(xué)過的特殊四邊形中是和美四邊形的例子.
![]() 如圖1,E,F,G,H分別是四邊形ABCD的邊AB,BC,CD,DA的中點(diǎn),已知四邊形EFGH是菱形,求證:四邊形ABCD是和美四邊形;
如圖1,E,F,G,H分別是四邊形ABCD的邊AB,BC,CD,DA的中點(diǎn),已知四邊形EFGH是菱形,求證:四邊形ABCD是和美四邊形;
![]() 如圖2,四邊形ABCD是和美四邊形,對(duì)角線AC,BD相交于O,
如圖2,四邊形ABCD是和美四邊形,對(duì)角線AC,BD相交于O,![]() ,E、F分別是AD、BC的中點(diǎn),請(qǐng)?zhí)剿?/span>EF與AC之間的數(shù)量關(guān)系,并證明你的結(jié)論.
,E、F分別是AD、BC的中點(diǎn),請(qǐng)?zhí)剿?/span>EF與AC之間的數(shù)量關(guān)系,并證明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩校的學(xué)生人數(shù)基本相同,為了解這兩所學(xué)校學(xué)生的數(shù)學(xué)學(xué)業(yè)水平,在同一次測(cè)試中,從兩校各隨機(jī)抽取了30名學(xué)生的測(cè)試成績(jī)進(jìn)行調(diào)查分析,其中甲校已經(jīng)繪制好了條形統(tǒng)計(jì)圖,乙校只完成了一部分.
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
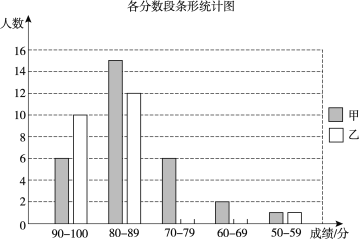
(1)請(qǐng)根據(jù)乙校的數(shù)據(jù)補(bǔ)全條形統(tǒng)計(jì)圖;
(2)兩組樣本數(shù)據(jù)的平均數(shù)、中位數(shù)、眾數(shù)如下表所示,請(qǐng)補(bǔ)全表格;
平均數(shù) | 中位數(shù) | 眾數(shù) | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)兩所學(xué)校的同學(xué)都想依據(jù)抽樣的數(shù)據(jù)說明自己學(xué)校學(xué)生的數(shù)學(xué)學(xué)業(yè)水平更好一些,
請(qǐng)為他們各寫出一條可以使用的理由;
甲校: .乙校: .
(4)綜合來看,可以推斷出 校學(xué)生的數(shù)學(xué)學(xué)業(yè)水平更好一些,理由為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】中華文明,源遠(yuǎn)流長(zhǎng);中華漢字,寓意深廣,為了傳承優(yōu)秀傳統(tǒng)文化,某校團(tuán)委組織了一次全校3000名學(xué)生參加的“漢字聽寫”大賽,賽后發(fā)現(xiàn)所有參賽學(xué)生的成績(jī)均不低于50分,為了更好地了解本次大賽的成績(jī)分布情況,隨機(jī)抽取了其中200名學(xué)生的成績(jī)(成績(jī)x取整數(shù),總分100分)作為樣本進(jìn)行整理,得到下列不完整的統(tǒng)計(jì)圖表:
成績(jī)x/分 | 頻數(shù) | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
請(qǐng)根據(jù)所給信息,解答下列問題: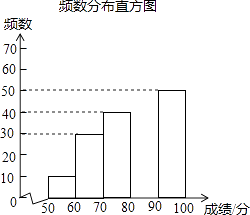
(1)m= , n=;
(2)請(qǐng)補(bǔ)全頻數(shù)分布直方圖;
(3)這次比賽成績(jī)的中位數(shù)會(huì)落在分?jǐn)?shù)段;
(4)若成績(jī)?cè)?0分以上(包括90分)的為“優(yōu)”等,則該校參加這次比賽的3000名學(xué)生中成績(jī)“優(yōu)”等約有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)如圖1,D1是△ABC的邊AB上的一點(diǎn),則圖中有哪幾個(gè)三角形?
(2)如圖2,D1,D2是△ABC的邊AB上的兩點(diǎn),則圖中有哪幾個(gè)三角形?
(3)如圖3,D1,D2,…,D10是△ABC的邊AB上的10個(gè)點(diǎn),則圖中共有多少個(gè)三角形?
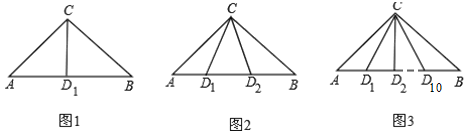
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“城市發(fā)展,交通先行”,我市啟動(dòng)了緩堵保暢的高架橋快速通道建設(shè)工程,建成后將大大提升道路的通行能力.研究表明,某種情況下,高架橋上的車流速度V(單位:千米/時(shí))是車流密度x(單位:輛/千米)的函數(shù),且當(dāng)0<x≤28時(shí),V=80;當(dāng)28<x≤188時(shí),V是x的一次函數(shù).函數(shù)關(guān)系如圖所示.
(1)求當(dāng)28<x≤188時(shí),V關(guān)于x的函數(shù)表達(dá)式;
(2)請(qǐng)你直接寫出車流量P和車流密度x之間的函數(shù)表達(dá)式;當(dāng)x為多少時(shí),車流量P(單位:輛/時(shí))達(dá)到最大,最大值是多少?
(注:車流量是單位時(shí)間內(nèi)通過觀測(cè)點(diǎn)的車輛數(shù),計(jì)算公式為:車流量=車流速度×車流密度)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com