
【題目】2018年暑期臨近,學生們也可輕松逛逛商場,選擇自己心儀的衣服![]() 安岳上府街一服裝店老板打算不錯失這一良機,計劃購進甲、乙兩種T恤
安岳上府街一服裝店老板打算不錯失這一良機,計劃購進甲、乙兩種T恤![]() 已知購進甲T恤2件和乙T恤3件共需310元;購進甲T恤1件和乙T恤2件共需190元
已知購進甲T恤2件和乙T恤3件共需310元;購進甲T恤1件和乙T恤2件共需190元
![]() 求甲、乙兩種T恤每件的進價分別是多少元?
求甲、乙兩種T恤每件的進價分別是多少元?
![]() 為滿足市場需求,服裝店需購進甲、乙兩種T恤共100件,要求購買兩種T恤的總費用不超過6540元,并且購買甲T恤的數量應小于購買甲乙兩種T恤總數量的
為滿足市場需求,服裝店需購進甲、乙兩種T恤共100件,要求購買兩種T恤的總費用不超過6540元,并且購買甲T恤的數量應小于購買甲乙兩種T恤總數量的![]() ,請你通過計算,確定服裝店購買甲乙兩種T恤的購買方案.
,請你通過計算,確定服裝店購買甲乙兩種T恤的購買方案.
【答案】(1) 甲種T恤每件進價為50元,乙種T恤每件進價為70元;(2)見解析.
【解析】
(1)設甲種商品每件的進價為x元,乙種商品每件的進價為y元,根據“購進甲商品2件和乙商品3件共需270元;購進甲商品3件和乙商品2件共需230元”可列出關于x、y的二元一次方程組,解方程組即可得出兩種商品的單價;(2)設商場購進甲種T恤a件,則購進乙種T恤為(100-a)件.根據“購買兩種T恤的總費用不超過6540元,并且購買甲T恤的數量應小于購買甲乙兩種T恤總數量的![]() ”列出不等式組并解答.
”列出不等式組并解答.
![]() 設甲種T恤每件進價為x元,乙種T恤每件進價為y元
設甲種T恤每件進價為x元,乙種T恤每件進價為y元![]() 由題意得
由題意得![]()
解得![]()
答:甲種T恤每件進價為50元,乙種T恤每件進價為70元.![]() 設商場購進甲種T恤a件,則購進乙種T恤為
設商場購進甲種T恤a件,則購進乙種T恤為![]() 件.
件.
根據題意得:
解得![]()
![]() 為整數,
為整數,![]() 為23或24
為23或24![]() 當
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]()
![]() 有兩種購買方案,方案一:購買甲種T恤23件,購買乙種T恤77件,
有兩種購買方案,方案一:購買甲種T恤23件,購買乙種T恤77件,
方案二:購買甲種T恤24件,購買乙種T恤76件.


科目:初中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,∠ABC=90,AE∥CD交BC于E,O是AC的中點,AB=![]() ,AD=2,BC=3,下列結論:
,AD=2,BC=3,下列結論:
①∠CAE=30;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正確的是()

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=BC,對角線BD平分∠ABC,P是BD上一點,過點P作PM⊥AD,PN⊥CD,垂足分別為M,N.

(1)求證:∠ADB=∠CDB;
(2)若∠ADC=90°,求證:四邊形MPND是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
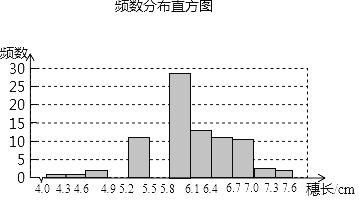
【題目】為了考察某種大麥細長的分布情況,在一塊試驗田里抽取了部分麥穗.測得它們的長度,數據整理后的頻數分布表及頻數分直方圖如下.根據以下信息,解答下列問題:
穗長x | 頻數 |
4.0≤x<4.3 | 1 |
4.3≤x<4.6 | 1 |
4.6≤x<4.9 | 2 |
4.9≤x<5.2 | 5 |
5.2≤x<5.5 | 11 |
5.5≤x<5.8 | 15 |
5.8≤x<6.1 | 28 |
6.1≤x<6.4 | 13 |
6.4≤x<6.7 | 11 |
6.7≤x<7.0 | 10 |
7.0≤x<7.3 | 2 |
7.3≤x<7.6 | 1 |
(Ⅰ)補全直方圖;
(Ⅱ)共抽取了麥穗 棵;
(Ⅲ)頻數分布表的組距是 ,組數是 ;
(Ⅳ)麥穗長度在5.8≤x<6.1范圍內麥穗有多少棵?占抽取麥穗的百分之幾?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在扇形OAB中,∠AOB=90°,正方形CDEF的頂點C是弧AB的中點,點D在OB上,點E在OB的延長線上,若正方形CDEF的邊長為2,則圖中陰影部分的面積為( ) 
A.π﹣2
B.2π﹣2
C.4π﹣4
D.4π﹣8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,動點P在平面直角坐標系中按圖中箭頭所示方向運動,第1次從原點運動到點(1,1),第2次接著運動到點(2,0),第3次接著運動到點(3,2),……,按這樣的運動規律,經過第100次運動后,動點P的坐標是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知, ![]() ,
, ![]() 與
與![]() 成正比例,
成正比例, ![]() 與
與![]() 成反比例,并且當
成反比例,并且當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() .
.
(![]() )求
)求![]() 關于
關于![]() 的函數關系式.
的函數關系式.
(![]() )當
)當![]() 時,求
時,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() .
.
【解析】分析:(1)首先根據![]() 與x成正比例,
與x成正比例, ![]() 與x成反比例,且當x=1時,y=4;當x=2時,y=5,求出
與x成反比例,且當x=1時,y=4;當x=2時,y=5,求出![]() 和
和![]() 與x的關系式,進而求出y與x的關系式,(2)根據(1)問求出的y與x之間的關系式,令y=0,即可求出x的值.
與x的關系式,進而求出y與x的關系式,(2)根據(1)問求出的y與x之間的關系式,令y=0,即可求出x的值.
本題解析:
(![]() )設
)設![]() ,
, ![]() ,
,
則![]() ,
,
∵當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
∴
解得, ![]() ,
,
∴![]() 關于
關于![]() 的函數關系式為
的函數關系式為![]() .
.
(![]() )把
)把![]() 代入
代入![]() 得,
得,
![]() ,
,
解得: ![]() ,
, ![]() .
.
點睛:本題考查了用待定系數法求反比例函數的解析式:(1)設出含有待定系數的反比例函數解析式y=kx(k為常數,k≠0);(2)把已知條件(自變量與對應值)代入解析式,得到待定系數的方程;(3)解方程,求出待定系數;(4)寫出解析式.
【題型】解答題
【結束】
24
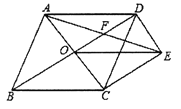
【題目】如圖,菱形![]() 的對角線
的對角線![]() 、
、![]() 相交于點
相交于點![]() ,過點
,過點![]() 作
作![]() 且
且![]() ,連接
,連接![]() 、
、![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)若菱形![]() 的邊長為2,
的邊長為2, ![]() .求
.求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
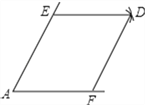
【題目】如圖,點E,F分別是銳角∠A兩邊上的點,AE=AF,分別以點E,F為圓心,以AE的長為半徑畫弧,兩弧相交于點D,連接DE,DF.
(1)請你判斷所畫四邊形的形狀,并說明理由;
(2)連接EF,若AE=8厘米,∠A=60°,求線段EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠A,∠B,∠C的對應邊分別是a,b,c,則滿足下列條件但不是直角三角形的是( )
A. ∠A=∠B-∠C B. ∠A:∠B:∠C=1:3:4 C. a:b:c=1:![]() :3 D.
:3 D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com