
【題目】將正面分別標有數字2,3,4的三張形狀、大小一樣的卡片洗勻后,背面朝上放在桌面上.
(1)隨機地抽取一張卡片,求抽到奇數的概率;
(2)隨機地抽取一張卡片,將卡片上標有的數字作為十位上的數字(不放回),再隨機地抽取一張卡片,將卡片上標有的數字作為個位上的數字,組成的兩位數恰好是“23”的概率是多少?
![]()
 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:初中數學 來源: 題型:
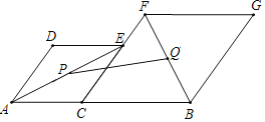
【題目】如圖,已知AB=2![]() ,C為線段AB上的一個動點,分別以AC,CB為邊在AB的同側作菱形ACED和菱形CBGF,點C,E,F在一條直線上,∠D=120°.P、Q分別是對角線AE,BF的中點,當點C在線段AB上移動時,點P,Q之間的距離最短為_____(結果保留根號).
,C為線段AB上的一個動點,分別以AC,CB為邊在AB的同側作菱形ACED和菱形CBGF,點C,E,F在一條直線上,∠D=120°.P、Q分別是對角線AE,BF的中點,當點C在線段AB上移動時,點P,Q之間的距離最短為_____(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】營養對促進中學生機體健康具有重要意義.現對一份學生快餐進行檢測,得到以下信息:

根據上述信息回答下面的問題:
(1)這份快餐中蛋白質和脂肪的質量共 克;
(2)分別求出這份快餐中脂肪、礦物質的質量;
(3)學生每餐膳食中主要營養成分“理想比”為:碳水化合物:脂肪:蛋白質=8:1:9,同時三者含量為總質量的90%.試判斷這份快餐中此三種成分所占百分比是否符合“理想比”?如果符合,直接寫出這份快餐中碳水化合物、脂肪、蛋白質、礦物質的質量比;如果不符合,求出符合“理想比”的四種成分中脂肪、礦物質的質量(總質量仍為300克).
查看答案和解析>>
科目:初中數學 來源: 題型:
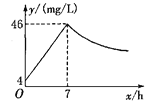
【題目】近年來,我國煤礦安全事故頻頻發生,其中危害最大的是瓦斯,其主要成分是CO.在一次礦難事件的調查中發現:從零時起,井內空氣中CO的濃度達到4 mg/L,此后濃度呈直線型增加,在第7小時達到最高值46 mg/L,發生爆炸;爆炸后,空氣中的CO濃度成反比例下降,如圖,根據題中相關信息回答下列問題:
(1)求爆炸前后空氣中CO濃度y與時間x的函數關系式,并寫出相應的自變量取值范圍;
(2)當空氣中的CO濃度達到34 mg/L時,井下3 km的礦工接到自動報警信號,這時他們至少要以多少km/h的速度撤離才能在爆炸前逃生?
(3)礦工只有在空氣中的CO濃度降到4 mg/L及以下時,才能回到礦井開展生產自救,求礦工至少在爆炸后多少小時才能下井?
查看答案和解析>>
科目:初中數學 來源: 題型:
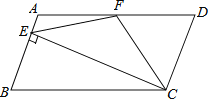
【題目】如圖,在ABCD中,AD=2AB,F是AD的中點,作CE⊥AB,垂足E在線段AB上,連接EF、CF,則下列結論中一定成立的是______.(把所有正確結論的序號都填在橫線上)①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB是⊙O的直徑,AT是⊙O的切線,∠ABT=50°,BT交⊙O于點C,E是AB上一點,延長CE交⊙O于點D.
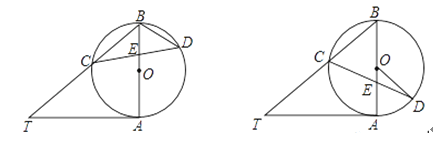
(1)如圖①,求∠T和∠CDB的大小;
(2)如圖②,當BE=BC,求∠CDO的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是∠AOB內任意一點,且∠AOB=40°,點M和點N分別是射線OA和射線OB上的動點,當△PMN周長取最小值時,則∠MPN的度數為( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中數學 來源: 題型:
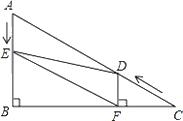
【題目】如圖,在Rt△ABC中,∠B=90°,BC=5![]() ,∠C=30°.點D從點C出發沿CA方向以每秒2個單位長的速度向點A勻速運動,同時點E從點A出發沿AB方向以每秒1個單位長的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(t>0).過點D作DF⊥BC于點F,連接DE、EF.
,∠C=30°.點D從點C出發沿CA方向以每秒2個單位長的速度向點A勻速運動,同時點E從點A出發沿AB方向以每秒1個單位長的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(t>0).過點D作DF⊥BC于點F,連接DE、EF.
(1)求證:AE=DF;
(2)四邊形AEFD能夠成為菱形嗎?如果能,求出相應的t值;如果不能,說明理由.
(3)當t為何值時,△DEF為直角三角形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,△ABC是等邊三角形,AE=CD,BQ⊥AD于Q,BE交AD于點P,下列說法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正確的個數有( )個。
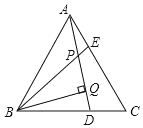
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com