
【題目】如圖,在平面直角坐標系中,坐標原點O是菱形ABCD的對稱中心.邊AB與x軸平行,點B(1,-2),反比例函數![]() (k≠0)的圖象經過A,C兩點.
(k≠0)的圖象經過A,C兩點.
(1)求點C的坐標及反比例函數的解析式.
(2)直線BC與反比例函數圖象的另一交點為E,求以O,C,E為頂點的三角形的面積.

【答案】(1)C(4,2),![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)連結AC,BD,根據坐標原點O是菱形ABCD的對稱中心,可得AC,BD相交于點O,且∠AOB=90°,根據B(1,﹣2),且AB∥x軸,可設A(a,﹣2),則AO2=a2+4,BO2=5,AB2=(1﹣a)2,在Rt△AOB中,由勾股定理可得A(﹣4,﹣2),C(4,2),再根據待定系數法可求反比例函數解析式;
(2)連結OE,則△OCE是以O,C,E為頂點的三角形,根據待定系數法可求直線BC的解析式,求出其與y軸交于點F的坐標,解方程可求點E的橫坐標,再根據三角形面積公式即可求解.
試題解析:解:(1)連結AC,BD,∵坐標原點O是菱形ABCD的對稱中心,∴AC,BD相交于點O,且∠AOB=90°,∵B(1,﹣2),且AB∥x軸,∴設A(a,﹣2),則AO2=a2+4,BO2=5,AB2=(1﹣a)2,在Rt△AOB中,由勾股定理得(1﹣a)2=a2+4+5,解得a=﹣4,∴A(﹣4,﹣2),∴C(4,2),∵反比例函數![]() (k≠0)的圖象經過A,C兩點,∴反比例函數解析式為
(k≠0)的圖象經過A,C兩點,∴反比例函數解析式為![]() ;
;
(2)連結OE,則△OCE是以O,C,E為頂點的三角形,設直線BC的解析式為y=kx+b,∵點B(1,﹣2),C(4,2)在該直線上,∴![]() ,解得:
,解得: 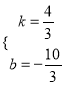 ,∴直線BC的解析式為
,∴直線BC的解析式為![]() ,設其與y軸交于點F(0,
,設其與y軸交于點F(0, ![]() ),∵反比例函數為
),∵反比例函數為![]() ,∴
,∴![]() ,解得x1=4,x2=
,解得x1=4,x2=![]() ,∴點E的橫坐標為
,∴點E的橫坐標為![]() ,∴以O,C,E為頂點的三角形的面積=
,∴以O,C,E為頂點的三角形的面積=![]() =
=![]() .
.



 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
【題目】下列正確說法的是____
①同位角相等; ②等角的補角相等; ③兩直線平行,同旁內角相等;④在同一平面內,過一點有且只有一條直線與已知直線垂直.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中.點E,F分別在BC,CD上,△AEF是等邊三角形.連接AC交EF于點G.過點G作GH⊥CE于點H.若![]() ,則
,則![]() =( )
=( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,則下列結論:
①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.
其中正確的結論有_______________(填結論前面的序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,以BC為直徑的圓分別交邊AC、AB于D、E兩點,連接BD、DE.若BD平分∠ABC,則下列結論不一定成立的是( )
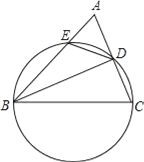
A. BD⊥AC B. AC2=2ABAE C. △ADE是等腰三角形 D. BC=2AD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】任意一個正整數都可以進行這樣的分解: ![]() (
(![]() 是正整數,且
是正整數,且![]() ),正整數的所有這種分解中,如果
),正整數的所有這種分解中,如果![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是正整數的最佳分解.并規定:
是正整數的最佳分解.并規定: ![]() .例如24可以分解成1×24,2×12,3×8或4×6,因為
.例如24可以分解成1×24,2×12,3×8或4×6,因為![]() ,所以4×6是24的最佳分解,所以
,所以4×6是24的最佳分解,所以![]() .
.
(1)求![]() 的值;
的值;
(2)如果一個兩位正整數, ![]() (
(![]() 為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差記為
為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差記為![]() ,交換其個位上的數與十位上的數得到的新數加上原來的兩位正整數所得的和記為
,交換其個位上的數與十位上的數得到的新數加上原來的兩位正整數所得的和記為![]() ,若
,若![]() 為4752,那么我們稱這個數為“最美數”,求所有“最美數”;
為4752,那么我們稱這個數為“最美數”,求所有“最美數”;
(3)在(2)所得“最美數”中,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習了二次根式后,小明同學發現有的二次根式可以寫成另一個二次根式的平方的形式.
比如: ![]() .善于動腦的小明繼續探究:
.善于動腦的小明繼續探究:
當![]() 為正整數時,若
為正整數時,若![]() ,則有
,則有![]() ,所以
,所以![]() ,
, ![]() .
.
請模仿小明的方法探索并解決下列問題:
(1)當![]() 為正整數時,若
為正整數時,若![]() ,請用含有
,請用含有![]() 的式子分別表示
的式子分別表示![]() ,得:
,得: ![]() ,
, ![]() ;
;
(2)填空: ![]()
![]()
- ![]() ;
;
(3)若![]() ,且
,且![]() 為正整數,求
為正整數,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com