
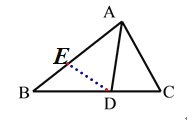
【題目】(10分)如圖①,在△ABC中,∠ACB=2∠B,AD為∠BAC的角平分線,
求證:AB=AC+CD
小明同學經過思考,得到如下解題思路:
在AB上截取AE=AC,連接DE,得到△ADE≌△ADC,從而易證AB=AC+CD
(1)請你根據以上解思路寫出證明過程;
(2)如圖②,若AD為△ABC的外角∠CAE平分線,交BC的延長線于點D,
∠D=25°,其他條件不變,求∠B的度數。


【答案】(1)見解析;(2)50°
【解析】試題分析:先根據“SAS”證明△ADE≌△ADC,從而DE=DC, ∠AED=∠ACB,再由外角的性質可得∠B=∠BDE,從而BE=CD,然后利用等量代換證明結論;(2)利用外角的性質和角平分線的定義得到∠CAD= ![]() ,然后根據三角形內角和列方程求解.
,然后根據三角形內角和列方程求解.
解:(1)∵AD為∠BAC的角平分線,
∴∠BAD=∠CAD.
在△ADE和△ADC中,
∵AC=AE,
∠BAD=∠CAD,
AD=AD,
∴△ADE≌△ADC,
∴DE=DC, ∠AED=∠ACB,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠BDE,
∴∠B=∠BDE,
∴BE=DE,
∴BE=CD.
∵AB=AE+BE,
∴AB=AC+CD.
(2)∵AD為∠BAC的角平分線,
∴∠CAD= ![]() .
.
∵∠ACB=2∠B,
∴∠CAE=∠ACB+∠B=3∠B, ∠BAC=180°-3∠B,
∴∠CAD= ![]() .
.
∴![]() ,
,
解之得
∠B=50°.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,線段![]() 和射線
和射線![]() 交于點
交于點![]() .
.
(![]() )利用尺規完成以下作圖,并保留作圖痕跡(不寫作法).
)利用尺規完成以下作圖,并保留作圖痕跡(不寫作法).
①在射線![]() 上作一點
上作一點![]() ,使
,使![]() ,連接
,連接![]() ;
;
②作![]() 的角平分線交
的角平分線交![]() 于
于![]() 點;
點;
③在射線![]() 上作一點
上作一點![]() ,使
,使![]() ,連接
,連接![]() .
.
(![]() )在(
)在(![]() )所作的圖形中,通過觀察和測量可以發現
)所作的圖形中,通過觀察和測量可以發現![]() ,請將下面的證明過程補充完整.
,請將下面的證明過程補充完整.

證明:∵![]() ,
,
∴![]() __________
__________![]() __________,①
__________,①
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() __________,②
__________,②
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .( )
.( )
查看答案和解析>>
科目:初中數學 來源: 題型:
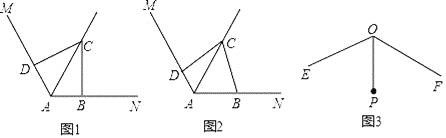
【題目】已知∠MAN=120°,點C是∠MAN的平分線AQ上的一個定點,點B,D分別在AN,AM上,連接BD.
【發現】
(1)如圖1,若∠ABC=∠ADC=90°,則∠BCD= °,△CBD是 三角形;
【探索】
(2)如圖2,若∠ABC+∠ADC=180°,請判斷△CBD的形狀,并證明你的結論;
【應用】
(3)如圖3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若點G,H分別在射線OE,OF上,且△PGH為等邊三角形,則滿足上述條件的△PGH的個數一共有 .(只填序號)
①2個②3個③4個④4個以上
查看答案和解析>>
科目:初中數學 來源: 題型:
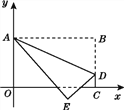
【題目】如圖,將長方形OABC置于平面直角坐標系中,點A的坐標為(0,4),點C的坐標為(m,0)(m>0),點D(m,1)在BC上,將長方形OABC沿AD折疊壓平,使點B落在坐標平面內,設點B的對應點為點E.
(1)當m=3時,點B的坐標為_________,點E的坐標為_________;
(2)隨著m的變化,試探索:點E能否恰好落在x軸上?若能,請求出m的值;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為深化義務教育課程改革,某校積極開展拓展性課程建設,設計開設藝術、體育、勞技、文學等多個類別的拓展性課程,要求每一位學生都自主選擇一個類別的拓展性課程。為了了解學生選擇拓展性課程的情況,隨機抽取了部分學生進行調查,并將調查結果繪制成如下統計圖(部分信息未給出):

根據統計圖中的信息,解答下列問題:
(1)求本次被調查的學生人數;
(2)將條形圖補充完整;
(3)若該校共有1600名學生,請估計全校選擇體育類的學生人數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如右圖,在每個小正方形邊長為1的方格紙中,△ABC的頂點都在方格紙格點上.將△ABC向左平移2格,再向上平移4格.
(1)請在圖中畫出平移后的△ABC,
(2)再在圖中畫出△ABC的高CD,
(3)在右圖中能使S△ABC=S△PBC的格點P的個數有 個(點P異于A)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com