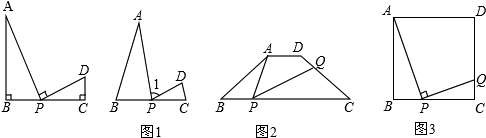
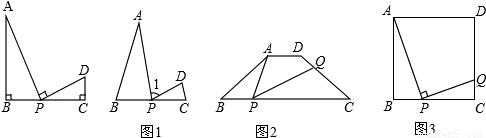
解:(1)成立,
∵∠A=180°-(∠B+∠APB),
∠CPD=180°-(∠1+∠APB),
∠B=∠1,
∴∠A=∠CPD,
∵∠B=∠C,
∴△ABP∽△PCD;
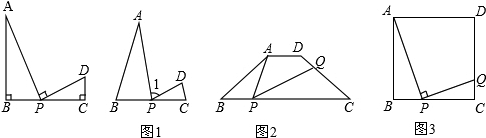
(2)①∵四邊形ABCD是等腰梯形,
∴∠B=∠C,
∵∠B=∠APQ,
∴∠B=∠APQ=∠C,
由(1)知,△ABP∽△PCD,
∴
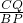
=

,
∴
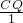
=

,
∴CQ=

;
②設BP=x,CQ=y.
∵∠B=∠APQ=90°,
∴△ABP∽△PCQ,
∴
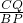
=

,即

=
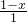
,
∴y=-x
2+x=-(x-

)
2+

,
∴當x=

時,y
最大=

,
即當P是BC的中點時,CQ最長,最長為

.
分析:(1)由∠A=180°-(∠B+∠APB)和∠CPD=180°-(∠1+∠APB),可得出∠B=∠1,則∠A=∠CPD,從而證明△ABP∽△PCD;
(2)①由四邊形ABCD是等腰梯形,則∠B=∠C,∠B=∠APQ=∠C,再由(1)知,△ABP∽△PCD,從而得出CQ;
②設BP=x,CQ=y.由∠B=∠APQ=90°,則△ABP∽△PCQ,再由相似三角形的性質,得出y與x之間的函數關系式,即y=-x
2+x=-(x-

)
2+

,根據二次函數的性質得出答案.
點評:本題考查了相似三角形的判定和性質、二次函數的最值問題、正方形的性質以及等腰三角形的性質,是一道綜合題,難度較大.

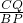 =
= ,
,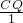 =
= ,
, ;
;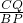 =
= ,即
,即 =
=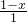 ,
, )2+
)2+ ,
, 時,y最大=
時,y最大= ,
, .
. )2+
)2+ ,根據二次函數的性質得出答案.
,根據二次函數的性質得出答案.