Question

如果有一個三位數的奇數，它除以11所得的商，是這個三位數的各位上的數的平方和，試求符合條件的所有三位數．

Answer 1

【答案】分析：首先根據已知得出要使a-b+c被11整除，其值只能是0和11，進而討論當a-b+c=0時，得9a+b=a²+b²+c²，以及當a-b+c=11時，得9a+b+1=a²+b²+c²．分別求出即可．
解答：解：設三位數為100a+10b+c，a，b，c都是整數，0＜a≤9，0≤b，c≤9，c為奇數，
那么 ，
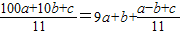
∵a最小是1，b最大是9，c最小是0，即可得出，-8＜a-b+c，
a最大是9，b最小是0，c最大是9，即可得出，a-b+c＜18．
∴-8＜a-b+c＜18，
要使a-b+c被11整除，其值只能是0和11，
（ 1）當a-b+c=0時，得9a+b=a²+b²+c²．
以b=a+c代入，并整理為關于a的二次方程，得
2a²+2（c-5）a+2c²-c=0
把c=1，3，5，7，9 逐一討論a的解
當c=1時，無整數解，當 c=3，5，7，9時，無實數根；
∴此時沒有滿足條件的三位奇數；

（2）當a-b+c=11時，得9a+b+1=a²+b²+c²．
以b=a+c-11代入，并整理為關于a的二次方程，得
2a²+2（c-16）a+2c²-23c+131=0．
把c=1，3，5，7，9 逐一討論a的解
當c=1時，無整數解，當 c=5，7，9時，無實數根；
只有當c=3時，a=8，b=0適合所有條件．
即所求三位數為803．
綜上所述，符合條件的三位數為803．
點評：此題主要考查了數的整除性以及整數的十進制表示法，根據已知得出a-b+c被11整除，其值只能是0和11是解題關鍵．
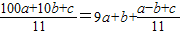