【題目】如圖，在
中，
，點
從點
出發沿
向點
運動，點
從點出發沿
向點運動，點和點同時出發，速度相同，到達點或點后運動停止．
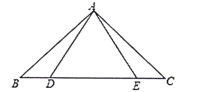
（1）求證：
；
（2）若
，求
的度數；
（3）若
的外心在其內部時，直接寫出
的取值范圍．
【答案】（1）證明見解析；（2）
；（3）
．
【解析】
（1）由題意得BD=CE，得出BE=CD，證出AB=AC，由SAS證明△ABE≌△ACD即可；
（2）由等腰三角形的性質和三角形內角和定理求出∠BEA=∠EAB=70°，作出AC=CD，由等腰三角形的性質得出∠ADC=∠DAC=70°，即可得出∠DAE的度數；
（3）對△ABD的外心位置進行推理，即可得出結論．
解：（1）∵點
、點
分別從點
、點
同時出發，在線段
上作等速運動，
∴
，
∴
，即
，
∵
，
∴
，
∴
（2）解：∵，
，
∴
∵
，
∴
，
∴
，
∴
（3）若△ABD的外心在其內部時，則△ABD是銳角三角形．
∴∠BAD=140°-∠BDA＜90°．
∴∠BDA＞50°，
又∵∠BDA＜90°，
∴50°＜∠BDA＜90°．
名校聯盟快樂課堂系列答案
黃岡創優卷系列答案科目：初中數學 來源： 題型：
【題目】（1）問題發現
如圖1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，連接AC，BD交于點M．填空：
①
的值為 ；
②∠AMB的度數為 ．
（2）類比探究
如圖2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，連接AC交BD的延長線于點M．請判斷的值及∠AMB的度數，并說明理由；
（3）拓展延伸
在（2）的條件下，將△OCD繞點O在平面內旋轉，AC，BD所在直線交于點M，若OD=1，OB=
，請直接寫出當點C與點M重合時AC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
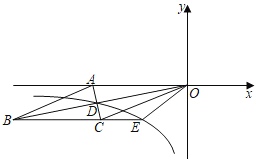
【題目】如圖，菱形OABC的一邊OA在x軸負半軸上．O是坐標原點，點A(﹣13，0)，對角線AC與OB相交于點D，且ACOB＝130，若反比例函數y＝
（x＜0）的圖象經過點D，并與BC的延長線交于點E．
（1）求雙曲線y＝的解析式；
（2）求S△AOB：S△OCE之值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某工程隊承接了60萬平方米的綠化工程，由于情況有變，…設原計劃每天綠化的面積為
萬平方米，列方程為
，根據方程可知省路的部分是（ ）
A.實際每天的工作效率比原計劃提高了
，結果提前30天完成了這一任務
B.實際每天的工作效率比原計劃提高了，結果延誤30天完成了這一任務
C.實際每天的工作效率比原計劃降低了，結果延誤30天完成了這一任務
D.實際每天的工作效率比原計劃降低了，結果提前30天完成了這一任務
查看答案和解析>>
科目：初中數學 來源： 題型：
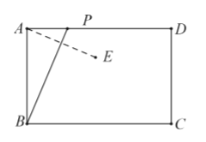
【題目】如圖，在矩形
中，
，
，點
是
上一動點，點
是點
關于直線
的對稱點，在點的運動過程中有且只有一個點到線段
的距離為4，則
的取值范圍是____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
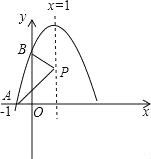
【題目】已知拋物線y=ax2+bx+3在坐標系中的位置如圖所示，它與x，y軸的交點分別為A，B，P是其對稱軸x=1上的動點，根據圖中提供的信息，給出以下結論：①2a+b=0，②x=3是ax2+bx+3=0的一個根，③△PAB周長的最小值是
+3
．其中正確的是（ ）
A. ①②③ B. 僅有①② C. 僅有①③ D. 僅有②③
查看答案和解析>>
科目：初中數學 來源： 題型：
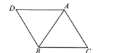
【題目】如圖，已知等邊
，
，將繞點A順時針旋轉
，得到
，點E是某邊的一點，當
為直角三角形時，連接
，作
于F，那么
的長度是_________________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，在平面直角坐標系中，拋物線y＝ax2＋bx＋c（a≠0）經過點D（2，4），與x軸交于A，B兩點，與y軸交于點C（0，4），連接AC，CD，BC， 其且AC=5．
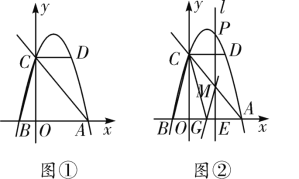
（1）求拋物線的解析式；
（2）如圖②，點P是拋物線上的一個動點，過點P作x軸的垂線l，l分別交x軸于點E，交直線AC于點M．設點P的橫坐標為m．當0<m≤2時，過點M作MG∥BC，MG交x軸于點G，連接GC，則m為何值時，△GMC的面積取得最大值，并求出這個最大值；
（3）當-1<m≤2時，是否存在實數m，使得以P，C，M為頂點的三角形和△AEM相似？若存在，求出相應m的值；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
