
【題目】在△ABC中,P是AB上的動點(P異于A、B),過點P的直線截△ABC,使截得的三角形與△ABC相似,我們不妨稱這種直線為過點P的△ABC的相似線,簡記為P(![]() ),(
),(![]() 為自然數)
為自然數)
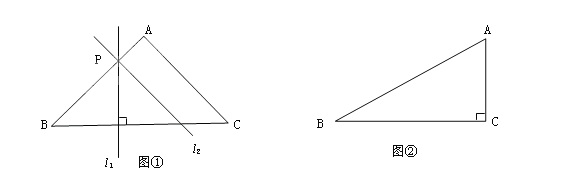
(1)如圖①,∠A=90°,∠B=∠C,當BP=2PA時,P(![]() )、P(
)、P(![]() )都是過點P的△ABC的相似線(其中
)都是過點P的△ABC的相似線(其中![]() ⊥BC,
⊥BC,![]() ∥AC),此外還有_______條.
∥AC),此外還有_______條.
(2)如圖②,∠C=90°,∠B=30°,當![]() _____時,P(
_____時,P(![]() )截得的三角形面積為△ABC面積的
)截得的三角形面積為△ABC面積的![]() .
.
【答案】(1)1;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
試題分析:(1)此外還有一條,如圖:過P點作平行于BC的直線,此時截得的三角形與△ABC相似,直線![]() 為過點P的△ABC的相似線;
為過點P的△ABC的相似線;
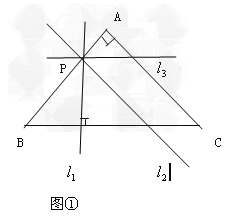
(2)若P(![]() )截得的三角形面積為△ABC面積的
)截得的三角形面積為△ABC面積的![]() .則截得的三角形與△ABC的相似比為
.則截得的三角形與△ABC的相似比為![]() ,①截得的三角形BP與AB是對應邊,AP與AB是對應邊,即當P為AB的中點時,過P點分別作平行于AC,BC的直線,則這兩條直線都滿足條件,如圖直線
,①截得的三角形BP與AB是對應邊,AP與AB是對應邊,即當P為AB的中點時,過P點分別作平行于AC,BC的直線,則這兩條直線都滿足條件,如圖直線![]() ,
,![]() ,此時
,此時![]() =
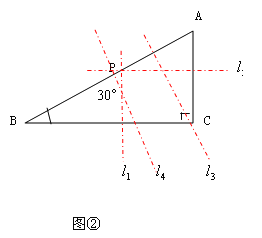
=![]() ;②截得的三角形BP與BC是對應邊,如圖直線
;②截得的三角形BP與BC是對應邊,如圖直線![]() ,此時
,此時![]() =
=![]() ,即
,即![]() =
=![]() ,化簡得:
,化簡得:![]() =
=![]() ×
×![]() =
=![]() ;③截得的三角形BP與BC是對應邊,如圖直線
;③截得的三角形BP與BC是對應邊,如圖直線![]() ,此時
,此時![]() =
=![]() ,即
,即![]() =
=![]() ,化簡得:
,化簡得:![]() =
=![]() ×
×![]() =
=![]() ;
;
綜上所述,當![]() =
=![]() 或
或![]() 或
或![]() 時P(
時P(![]() )截得的三角形面積為△ABC面積的
)截得的三角形面積為△ABC面積的![]() .
.


科目:初中數學 來源: 題型:
【題目】計劃建一個長方形養雞場,為了節省材料,利用一道足夠長的墻做為養雞場的一邊,另三邊用鐵絲網圍成,如果鐵絲網的長為35m.
(1)計劃建養雞場面積為150m2,則養雞場的長和寬各為多少?
(2)能否建成的養雞場面積為160m2?如果能,請算出養雞場的長和寬;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:關于x的方程x2-2(m+1)x+m2=0.
(1)當m取何值時,方程有兩個實數根?
(2)為m選取一個合適的整數,使方程有兩個不相等的實數根,并求這兩個根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)試說明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如圖2,動點M從點B出發以每秒2cm的速度沿線段BA向點A 運動,同時動點N從點A出發以每秒1cm速度沿線段AC向點C運動,當其中一點到達終點時整個運動都停止. 設點M運動的時間為t(秒),
①若△DMN的邊與BC平行,求t的值;
②若點E是邊AC的中點,問在點M運動的過程中,△MDE能否成為等腰三角形?若能,求出t的值;若不能,請說明理由.
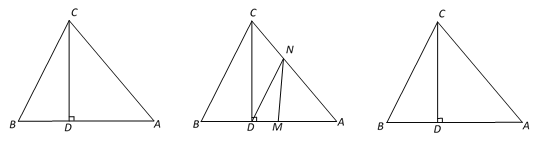
圖1 圖2 備用圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某科技開發公司研制出一種新型產品,每件產品的成本為2400元,銷售單價定為3000元.在該產品的試銷期間,為了促銷,鼓勵商家購買該新型產品,公司決定商家一次購買這種新型產品不超過10件時,每件按3000元銷售;若一次購買該種產品超過10件時,每多購買一件,所購買的全部產品的銷售單價均降低10元,但銷售單價均不低于2600元.
(1)商家一次購買這種產品多少件時,銷售單價恰好為2600元?
(2)設商家一次購買這種產品x件,開發公司所獲的利潤為y元,求y(元)與x(件)之間的函數關系式,并寫出自變量x的取值范圍.
(3)該公司的銷售人員發現:當商家一次購買產品的件數超過某一數量時,會出現隨著一次購買的數量的增多,公司所獲的利潤反而減少這一情況.為使商家一次購買的數量越多,公司所獲的利潤最大,公司應將最低銷售單價調整為多少元(其它銷售條件不變)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=10,AC=8,BC=6,以邊AB的中點O為圓心,作半圓與AC相切,點P,Q分別是邊BC和半圓上的動點,連接PQ,則PQ長的最大值與最小值的和是( )
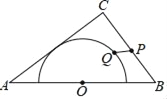
A. 9 B. 10 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)如圖,在五邊形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求證:△ABC≌△AED;
(2)當∠B=140°時,求∠BAE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
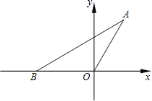
【題目】如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,
,![]() 的面積是
的面積是![]() .
.
![]() 求點
求點![]() 的坐標;
的坐標;
![]() 求過點
求過點![]() 、
、![]() 、
、![]() 的拋物線的解析式;
的拋物線的解析式;
![]() 在
在![]() 中拋物線的對稱軸上是否存在點
中拋物線的對稱軸上是否存在點![]() ,使
,使![]() 的周長最小?若存在,求出點
的周長最小?若存在,求出點![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
![]() 在
在![]() 中
中![]() 軸下方的拋物線上是否存在一點
軸下方的拋物線上是否存在一點![]() ,過點
,過點![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點
于點![]() ,線段
,線段![]() 把
把![]() 分成兩個三角形,使其中一個三角形面積與四邊形
分成兩個三角形,使其中一個三角形面積與四邊形![]() 面積比為
面積比為![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com