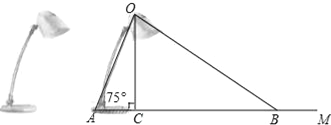
【題目】如圖為放置在水平桌面上的臺燈的平面示意圖，燈臂AO長為40cm，與水平面所形成的夾角∠OAM為75°．由光源O射出的邊緣光線OC，OB與水平面所形成的夾角∠OCA，∠OBA分別為90°和30°，求該臺燈照亮水平面的寬度BC（不考慮其他因素，結果精確到0.1cm．溫馨提示：sin75°≈0.97，cos75°≈0.26，
≈1.73）．
科目：初中數學 來源： 題型：
【題目】如圖1，有若干張邊長為
的小正方形①、長為
寬為的長方形②以及邊長為的大正方形③的紙片．
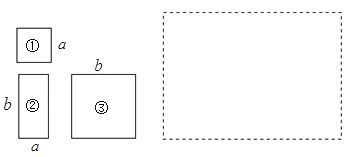
（1）已知小正方形①與大正方形③的面積之和為169，長方形②的周長為34，求長方形②的面積．
（2）如果現有小正方形①1張，大正方形③2張，長方形②3張，請你將它們拼成一個大長方形 （在圖2虛線框內畫出圖形），并運用面積之間的關系，將多項式
分解因式．
查看答案和解析>>
科目：初中數學 來源： 題型：
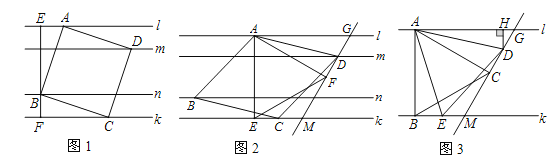
【題目】【背景】已知：l∥m∥n∥k，平行線l與m、m與n、n與k之間的距離分別為d1，d2，d3，且d1＝d3＝1，d2＝2.我們把四個頂點分別在l，m，n，k這四條平行線上的四邊形稱為“格線四邊形” ．
【探究1】(1)如圖1，正方形ABCD為“格線四邊形”，BE⊥l于點E，BE的反向延長線交直線k于點F.求正方形ABCD的邊長．
【探究2】(2)如圖2，菱形ABCD為“格線四邊形”且∠ADC＝60°，△AEF是等邊三角形，AE⊥k于點E，∠AFD＝90°，直線DF分別交直線l，k于點G、點M.求證：EC＝DF．
【拓展】(3)如圖3，l∥k，等邊△ABC的頂點A，B分別落在直線l，k上，AB⊥k于點B，且∠ACD＝90°，直線CD分別交直線l、k于點G、點M，點D、點E分別是線段GM、BM上的動點，且始終保持AD＝AE，DH⊥l于點H.猜想：DH在什么范圍內，BC∥DE？并說明此時BC∥DE的理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】 某檢修小組從A地出發，在東西向的馬路上檢修線路，如果規定向東行駛為正，向西行駛為負，一天中七次行駛紀錄如下.（單位：km）
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
－4 | ＋7 | －9 | ＋8 | ＋6 | －5 | －2 |
(1)求收工時距A地多遠？
(2)在第 次紀錄時距A地最遠.
(3)若每km耗油0.3升，問共耗油多少升？
查看答案和解析>>
科目：初中數學 來源： 題型：
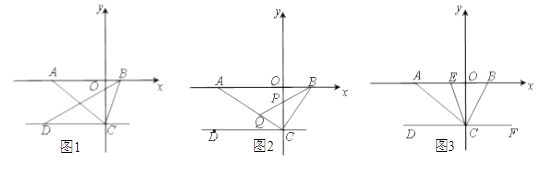
【題目】如圖1，在平面直角坐標系中，點
為
軸負半軸上一點，點
為軸正半軸上一點，
，
，其中
，
滿足關系式：
＋
.
（1）= ，= ，△
的面積為 ；
（2）如圖2，若
⊥
，點
線段
上一點，連接
，延長交于點
，當∠
=∠
時，求證:平分∠
；
（3）如圖3，若⊥，點
是點與點之間一動點，連接
,
始終平分∠
,當點在點與點之間運動時，
的值是否變化？若不變，求出其值；若變化，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，對于任意兩點A（x1，y1）B （x2，y2），規定運算：
（1）A⊕B=（x1+x2，y1+y2）；
（2）A⊙B=x1x2+y1y2；
（3）當x1=x2且y1=y2時，A=B．
有下列四個命題：
①若有A（1，2），B（2，﹣1），則A⊕B=（3，1），A⊙B=0；
②若有A⊕B=B⊕C，則A=C；
③若有A⊙B=B⊙C，則A=C；
④（A⊕B）⊕C=A⊕（B⊕C）對任意點A、B、C均成立．
其中正確的命題為______（只填序號）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
