【題目】列一元一次方程解答下列問題：
(1)義烏市為了搞好“五水共治”工作，將一段長為
的河道任務交由甲乙兩個工程隊先后接力完成，共用時20天，已知甲工程隊每天整治
，乙工程隊每天整治
，試求甲乙兩個工程隊分別整治了多長的河道.
(2)小玲在數學書上發現如圖所示的題目，兩個方框表示的是同一個數，請你幫小玲求出方框所表示的數.
【答案】(1)甲工程隊整治了
，乙工程隊整治了
；(2)2.
【解析】
（1）根據題意利用一段為3600m的河道整治任務，由甲、乙兩個工程隊先后接力完成，進而表示出兩工程隊完成的總米數得出等式，求出即可．
（2）設方框里的數為x，根據題意列出方程即可求解.
（1）設甲工程隊做了x天，則乙工程隊做了（20-x）天，
根據題意可得：240x+160（20-x）=3600，
解得：x=5，
故甲工程隊整治了5×240=1200（m），乙工程隊整治了160×15=2400（m）．
答：甲工程隊整治了1200m的河道，乙工程隊整治了2400m的河道．
（2）設方框里的數為x，根據題意得：12×（460+x）=（100x+64）×21
解得：x=2
∴方框內的數是2
科目：初中數學 來源： 題型：
【題目】如圖，AB為半圓O的直徑，C為AO的中點，CD⊥AB交半圓于點D，以C為圓心，CD為半徑畫弧交AB于E點，若AB＝4，則圖中陰影部分的面積是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某印刷廠有甲、乙兩種收費方式，除按印數收取印刷費外，甲種方式還需收取制版費而乙種不需要．兩種印刷方式的費用y（元）與印刷份數x（份）之間的關系如圖所示：
（1）填空：甲種收費的函數表達式是 ，乙種收費的函數表達式是 ．
（2）請你根據不同的印刷數量幫忙確定選擇哪種印刷方式較合算.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料:對于排好順序的三個數:
稱為數列.將這個數列如下式進行計算: 
，
，
，所得的三個新數中，最大的那個數稱為數列的“關聯數值”.
例如：對于數列
因為
所以數列的“關聯數值”為6.進一步發現:當改變這三個數的順序時，所得的數列都可以按照上述方法求出“關聯數值”，如:數列
的 “關聯數值”為0；數列
的“關聯數值”為3...而對于“
”這三個數，按照不同的排列順序得到的不同數列中，“關聯數值"的最大值為6.
（1）數列
的“關聯數值”為_______；
（2）將“”這三個數按照不同的順序排列，可得到若干個不同的數列，這些數列的“關聯數值”的最大值是_______， 取得“關聯數值”的最大值的數列是______
（3）將“
”
這三個數按照不同的順序排列，可得到若干個不同的數列，這些數列的“關聯數值”的最大值為10，求
的值，并寫出取得“關聯數值”最大值的數列.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】．如圖，矩形ABCD中，O為AC中點，過點O的直線分別與AB、CD交于點E、F，連結BF交AC于點M，連結DE、BO．若∠COB=60°，FO=FC，則下列結論：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正確結論的個數是（ ）
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目：初中數學 來源： 題型：
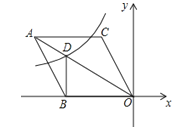
【題目】如圖，在平面直角坐標系中，菱形ABOC的頂點O在坐標原點，邊BO在x軸的負半軸上，∠BOC=60°，頂點C的坐標為（m，
），反比例函數
的圖像與菱形對角線AO交于D點，連接BD，當BD⊥x軸時，k的值是（ ）
A. 
B. － C. 
D. －
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，半徑為1個單位的圓片上有一點A與數軸上的原點重合，AB是圓片的直徑．(注：結果保留π )
(1)把圓片沿數軸向右滾動半周，點B到達數軸上點C的位置，點C表示的數是 數(填“無理”或“有理”)，這個數是 ；
(2)把圓片沿數軸滾動2周，點A到達數軸上點D的位置，點D表示的數是 ；
(3)圓片在數軸上向右滾動的周數記為正數，圓片在數軸上向左滾動的周數記為負數，依次運動情況記錄如下：+2，﹣1，+3，﹣4，﹣3．
①第 次滾動后，A點距離原點最近，第 次滾動后，A點距離原點最遠．
②當圓片結束運動時，A點運動的路程共有 ，此時點A所表示的數是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司從2014年開始投入技術改進資金，經技術改進后，其產品的成本不斷降低，具體數據如下表：
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改資金 | 2.5 | 3 | 4 | 4.5 |
產品成本 | 7.2 | 6 | 4.5 | 4 |
（1）請你認真分析表中數據，從一次函數和反比例函數中確定哪一個函數能表示其變化規律，給出理由，并求出其解析式；
（2）按照這種變化規律，若2017年已投入資金5萬元.
①預計生產成本每件比2016年降低多少萬元？
②若打算在2017年把每件產品成本降低到3.2萬元，則還需要投入技改資金多少萬元？（結果精確到0.01萬元）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，坡AB的坡比為1：2.4，坡長AB=130米，坡AB的高為BT．在坡AB的正面有一棟建筑物CH，點H、A、T在同一條地平線MN上．
（1）試問坡AB的高BT為多少米？
（2）若某人在坡AB的坡腳A處和中點D處，觀測到建筑物頂部C處的仰角分別為60°和30°，試求建筑物的高度CH．（精確到米， 
≈1.73， 
≈1.41）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
