
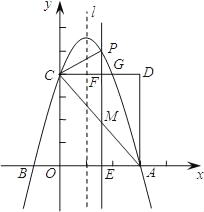
【題目】如圖,拋物線y=ax2﹣2ax+c(a≠0)交x軸于A、B兩點,A點坐標為(3,0),與y軸交于點C(0,4),以OC、OA為邊作矩形OADC交拋物線于點G.
(1)求拋物線的解析式;
(2)拋物線的對稱軸l在邊OA(不包括O、A兩點)上平行移動,分別交x軸于點E,交CD于點F,交AC于點M,交拋物線于點P,若點M的橫坐標為m,請用含m的代數式表示PM的長;
(3)在(2)的條件下,連結PC,則在CD上方的拋物線部分是否存在這樣的點P,使得以P、C、F為頂點的三角形和△AEM相似?若存在,求出此時m的值,并直接判斷△PCM的形狀;若不存在,請說明理由.
【答案】(1)拋物線的解析式為y=﹣![]() x2+
x2+![]() x+4;(2)PM=﹣
x+4;(2)PM=﹣![]() m2+4m(0<m<3);(3)存在這樣的點P使△PFC與△AEM相似,此時m的值為
m2+4m(0<m<3);(3)存在這樣的點P使△PFC與△AEM相似,此時m的值為![]() 或1,△PCM為直角三角形或等腰三角形.
或1,△PCM為直角三角形或等腰三角形.
【解析】試題分析:(1)將A(3,0),C(0,4)代入y=ax2-2ax+c,運用待定系數法即可求出拋物線的解析式;
(2)先根據A、C的坐標,用待定系數法求出直線AC的解析式,進而根據拋物線和直線AC的解析式分別表示出點P、點M的坐標,即可得到PM的長;
(3)由于∠PFC和∠AEM都是直角,F和E對應,則若以P、C、F為頂點的三角形和△AEM相似時,分兩種情況進行討論:①△PFC∽△AEM,②△CFP∽△AEM;可分別用含m的代數式表示出AE、EM、CF、PF的長,根據相似三角形對應邊的比相等列出比例式,求出m的值.
試題解析:(1)∵拋物線y=ax2-2ax+c(a≠0)經過點A(3,0),點C(0,4),
∴![]() ,
,
解得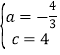 .
.
∴拋物線的解析式為y=-![]() x2+
x2+![]() x+4;
x+4;
(2)設直線AC的解析式為y=kx+b,
∵A(3,0),點C(0,4),
∴![]() ,
,
解得 .
.
∴直線AC的解析式為y=-![]() x+4.
x+4.
∵點M的橫坐標為m,點M在AC上,
∴M點的坐標為(m,-![]() m+4),
m+4),
∵點P的橫坐標為m,點P在拋物線y=-![]() x2+
x2+![]() x+4上,
x+4上,
∴點P的坐標為(m,-![]() m2+
m2+![]() m+4),
m+4),
∴PM=PE-ME=(-![]() m2+
m2+![]() m+4)-(-
m+4)-(-![]() m+4)=-
m+4)=-![]() m2+4m,
m2+4m,
即PM=-![]() m2+4m(0<m<3);
m2+4m(0<m<3);
(3)在(2)的條件下,連結PC,在CD上方的拋物線部分存在這樣的點P,使得以P、C、F為頂點的三角形和△AEM相似.理由如下:由題意,可得AE=3-m,EM=-![]() m+4,CF=m,若以P、C、F為頂點的三角形和△AEM相似,情況:
m+4,CF=m,若以P、C、F為頂點的三角形和△AEM相似,情況:
①P點在CD上方,則PF=-![]() m2+
m2+![]() m+4-4=-
m+4-4=-![]() m2+
m2+![]() m.
m.
若△PFC∽△AEM,則PF:AE=FC:EM,
即(-![]() m2+
m2+![]() m):(3-m)=m:(-
m):(3-m)=m:(-![]() m+4),
m+4),
∵m≠0且m≠3,
∴m=![]() ;
;
②若△CFP∽△AEM,則CF:AE=PF:EM,
即m:(3-m)=(-![]() m2+
m2+![]() m):(-
m):(-![]() m+4),
m+4),
∵m≠0且m≠3,
∴m=1.
綜上所述,存在這樣的點P使△PFC與△AEM相似.此時m的值為![]() 或1.
或1.


 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
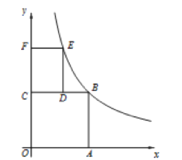
【題目】如圖,正方形OABC的邊OA,OC在坐標軸上,矩形CDEF的邊CD在CB上,且5CD=3CB,邊CF在軸上,且CF=2OC-3,反比例函數y=![]() (k>0)的圖象經過點B,E,則點E的坐標是____
(k>0)的圖象經過點B,E,則點E的坐標是____
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,函數![]() 的圖象與函數
的圖象與函數![]() 的圖象交于點
的圖象交于點![]() ,
,![]() .
.
(1)求函數![]() 的表達式;
的表達式;
(2)觀察圖象,直接寫出不等式![]() 的解集;
的解集;
(3)若點![]() 是
是![]() 軸上的動點,當
軸上的動點,當![]() 周長最小時,求點
周長最小時,求點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點 E,F 是ABCD 對角線上兩點,在條件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一個條件,使四邊形 DEBF 是平行四邊形,可添加 的條件是( )
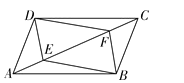
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】書店舉行購書優惠活動:
①一次性購書不超過100元,不享受打折優惠;
②一次性購書超過100元但不超過200元,一律按原價打九折;
③一次性購書超過200元,一律按原價打七折.
小麗在這次活動中,兩次購書總共付款229.4元,第二次購書原價是第一次購書原價的3倍,那么小麗這兩次購書原價的總和是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線l1:![]() 分別與x軸、y軸交于點B、C,且與直線l2:
分別與x軸、y軸交于點B、C,且與直線l2:![]() 交于點A.
交于點A.
(1)求出點A的坐標
(2)若D是線段OA上的點,且△COD的面積為12,求直線CD的解析式
(3)在(2)的條件下,設P是射線CD上的點,在平面內是否存在點Q,使以O、C、P、Q為頂點的四邊形是菱形?若存在,直接寫出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某人出去散步,從家里出發,走了20min,到達一個離家900m的閱報亭,看了10min報紙后,用了15min返回家里,下面圖象中正確表示此人離家的距離y(m)與時間x(min)之家關系的是( )
A.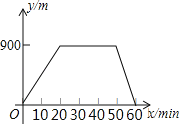 B.
B.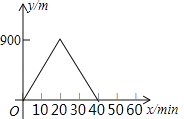
C.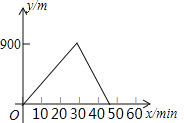 D.
D.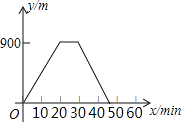
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以四邊形ABCD的邊AB、AD為底邊分別作等腰三角形ABF和ADE,連接EB.
(1)當四邊形ABCD為正方形時(如圖1),以邊AB、AD為斜邊分別向外側作等腰直角三角形ABF和ADE,連接EB、FD,線段EB和FD的數量關系是 .
(2)當四邊形ABCD為矩形時(如圖2),以邊AB、AD為斜邊分別向內側作等腰直角三角形ABF和ADE,連接EF、BD,線段EF和BD具有怎樣的數量關系?請加以證明;
(3)當四邊形ABCD為平行四邊形時(如圖3),以邊AB、AD為斜邊分別向平行四邊形內測、外側作等腰直角三角形ABF和ADE,且△EAD與△FBA的頂角都為α,連接EF、BD,交點為G,請用α表示出∠EGD,并說明理由.
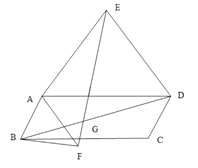
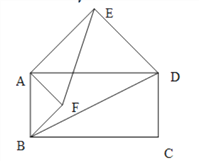
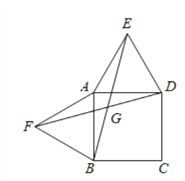
圖1 圖2 圖3
【答案】(1)EF=BD;(2)EF=![]() BD;(3)
BD;(3)![]()
【解析】分析:(1)正方形的性質、等邊三角形的性質和全等三角形的證明方法可證明△AFD≌△ABE,由全等三角形的性質即可得到EB=FD;(2)根據等腰直角三角形的性質可得![]() ,再證得∠BAD=∠FAE,即可判定△BAD∽△FAE ,根據相似三角形的性質可得
,再證得∠BAD=∠FAE,即可判定△BAD∽△FAE ,根據相似三角形的性質可得![]() ,即可得
,即可得![]() ;(3)
;(3)![]() ,先證△BFA∽△DEA,即可得
,先證△BFA∽△DEA,即可得![]() ,
,
再證得![]() ,所以△BAD∽△FAE,根據全等三角形的性質即可得
,所以△BAD∽△FAE,根據全等三角形的性質即可得![]() ,再由∠AHE=∠DHG,即可得
,再由∠AHE=∠DHG,即可得![]() .
.
詳解:(1)EF=BD,
理由如下:
四邊形ABCD為正方形,
∴AB=AD,
∵以四邊形ABCD的邊AB、AD為邊分別向外側作等邊三角形ABF和ADE,
∴AF=AE,∠FAB=∠EAD=60°,
∵∠FAD=∠BAD+∠FAB=90°+60°=150°,
∠BAE=∠BAD+∠EAD=90°+60°=150°,
∴∠FAD=∠BAE,
在△AFD和△ABE中, 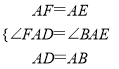 ,
,
∴△AFD≌△ABE,
∴EB=FD;
(2)EF=![]() BD.
BD.
證明:∵△AFB為等腰直角三角形
∴![]() ,∠FAB=45°
,∠FAB=45°
同理: ![]() ,∠EAD=45° ∴∠BAD+∠FAD=∠EAD+∠DAF
,∠EAD=45° ∴∠BAD+∠FAD=∠EAD+∠DAF
即∠BAD=∠FAE
∵![]() ,
, ![]() ∴
∴![]()
∴△BAD∽△FAE ∴![]()
即: ![]()
(3)解: ![]()
∵△AFB為等腰直角三角形,∴FB=FA,
同理:ED=EA,∴![]() ,
,
又∵![]() ,∴△BFA∽△DEA,
,∴△BFA∽△DEA,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△BAD∽△FAE,
∴![]() ,
,
又∵∠AHE=∠DHG,
∴![]() .
.
點睛:本題考查了正方形的性質、全等三角形的判定和性質、等邊三角形的性質等腰直角三角形的先證、相似三角形的判定和性質,題目的綜合性很強,難度也不小,解題的關鍵是對特殊幾何圖形的性質要準確掌握.
【題型】解答題
【結束】
27
【題目】如圖,二次函數![]() 的圖象交x軸于A、B兩點,交y軸于點C,點B的坐標為(3,0),頂點C的坐標為(1,4).連接BC.
的圖象交x軸于A、B兩點,交y軸于點C,點B的坐標為(3,0),頂點C的坐標為(1,4).連接BC.
(1)求二次函數的解析式和直線BC的解析式;
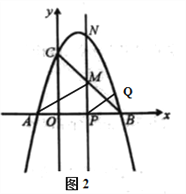
(2)點M是直線BC上的一個動點(不與B、C重合),過點M作x軸的垂線,交拋物線于點N,交x軸于點P.
①如圖1,求線段MN長度的最大值;
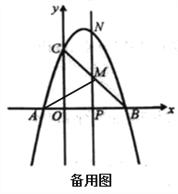
②如圖2,連接AM,QN,QP.試問:拋物線上是否存在點Q,使得![]() 與
與![]() 的面積相等,且線段NQ的長度最小?如果存在,求出點Q的坐標;如果不存在,請說明理由.
的面積相等,且線段NQ的長度最小?如果存在,求出點Q的坐標;如果不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A(a ,2![]() )是直線y=
)是直線y=![]() x上一點,以A為圓心,2為半徑作⊙A,若P(x,y)是第一象限內⊙A上任意一點,則
x上一點,以A為圓心,2為半徑作⊙A,若P(x,y)是第一象限內⊙A上任意一點,則![]() 的最小值為( )
的最小值為( )
A. 1 B. ![]() C.
C. ![]() —1 D.
—1 D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com