Question

等腰梯形的周長為60，腰長為8，對角線長為24，則連接兩腰中點與一底中點的線段組成的三角形的周長為    ．

Answer 1

【答案】分析：簡單的畫出圖形，等腰梯形對角線相等，利用中位線求出三角形各邊長，進而可求解其周長．
解答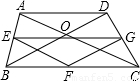：解：如圖，
因為E，F，G分別為AB，BC，CD中點，
所以EF=AC，FG=BD，EG=（AD+BC）
又等腰梯形的周長為60，腰長為8，所以AD+BC=60-8×2=44
AC=BD=24
∴三角形EFG的周長為EF+FG+GE=AC+BD+（AD+BC）=12+12+22=46．
點評：熟練掌握等腰梯形的性質，能夠求解一些簡單的計算問題．