Question

（本小題滿分12分）
如圖，RtΔABC中，∠ACB=90°，AC=4，BA=5，點P是AC上的動點（P不與A、C重合）PQ⊥AB，垂足為Q．設PC=x，PQ= y．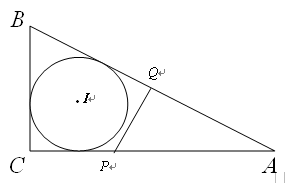

【小題1】⑴求y與x的函數關系式；
【小題2】⑵試確定此RtΔABC內切圓I的半徑，并探求x為何值時，直線PQ與這個內切圓I相切？
【小題3】⑶若0<x<1，試判斷以P為圓心，半徑為y的圓與⊙I能否相內切，若能求出相應的x的值，若不能，請說明理由．

Answer 1

【小題1】⑴如圖1，PQ=y
 ∵∠A=∠A，∠ACB=∠AQP=90°
 ∴RtΔAQP∽ΔRtΔACB，
∴PQ∶BC=AP∶AB
依題意可得：BC=3，AP=4－x
∴   
化簡得：
【小題2】⑵假設直線PQ與這個內切圓I能相切，令切點為M，如圖，
可知四邊形IMQN也是正方形，
則有PM=PE，MQ=IN=1,
∴ PC=PQ，
即 x=y，
又  
解之，得x=.
【小題3】⑶當⊙P與⊙I內切時，如圖3，
根據勾股定理得：
即  
將代入得

解之得.

解析