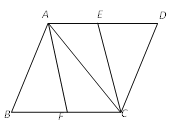
【題目】如圖，在□ABCD中，E、F分別是AD、BC的中點，連接AC、CE、AF．
（1）求證△ABF ≌ △CDE；
（2）若AB＝AC，求證四邊形AFCE是矩形．
【答案】(1)證明見解析；（2）證明見解析
【解析】試題分析：(1)、根據平行四邊形的性質得出AB=CD，AD=BC，∠B=∠D，根據中點的性質得出BF=DE，最后根據SAS判定出三角形全等；(2)、首先根據全等以及中點的性質得出四邊形AFCE為平行四邊形，根據等腰三角形的性質得出AF⊥BC，從而得出矩形.
試題解析：（1）、∵ 四邊形ABCD是平行四邊形，∴ AB＝CD,AD＝BC，∠B＝∠D．
∵ E、F分別是AD、BC的中點， ∴ DE＝AE＝ 
AD， BF＝CF＝ BC．∴ BF＝DE，CF＝AE．
∴ △ABF≌△CDE(SAS)．
（2）∵△ABF≌△CDE(SAS)， ∴ AF＝CE． 又∵CF＝AE，
∴四邊形AFCE是平行四邊形． ∵AB＝AC, F分別是BC的中點， ∴AF⊥BC．
即∠AFC＝90°． ∴四邊形AFCE是矩形．
科目：初中數學 來源： 題型：
【題目】某校九年級有15名同學參加校運會百米比賽，預賽成績各不相同，前7名才有資格參加決賽，小明已經知道了自己的成績，但他想知道自己能否進入決賽，還需要知道這15名同學成績的_____．（填“極差”、“眾數”或“中位數”）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】買一個足球需要m元，買一個籃球需要n元，則買4個足球、7個籃球共需（ ）
A．28mn 元 B．11mn元 C．（7m+4n）元 D．（4m+7n）元
查看答案和解析>>
科目：初中數學 來源： 題型：
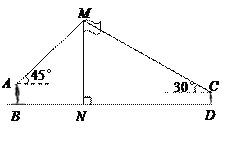
【題目】如圖，某數學興趣小組在活動課上測量學校旗桿高度．已知小明的眼睛與地面的距離AB=1.7m，看旗桿頂部
的仰角為
；小紅的眼睛與地面的距離CD=1.5m，看旗桿頂部
的仰角為
．兩人相距28米且位于旗桿兩側（點B、N、D在同一條直線上）．請求出旗桿
的高度．（參考數據： 
， 
，結果保留整數）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，過邊長為1的等邊△ABC的邊AB上一點P，作PE⊥AC于E，Q為BC延長線上一點，當PA=CQ時，連PQ交AC邊于D，則DE的長為（ ）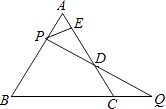 
A.
B.
C.
D.不能確定
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】王華、張偉兩位同學分別將自己10次數學自我檢測的成績繪制成如下統計圖：
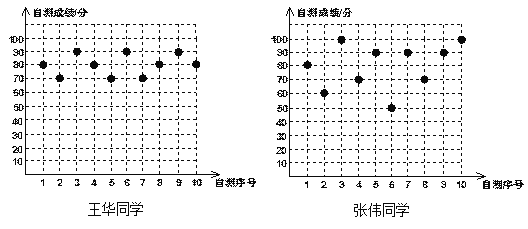
（1）根據上圖中提供的數據列出如下統計表：
平均成績（分） | 中位數（分） | 眾數（分） | 方差（S2） | |
王華 | 80 | b | 80 | d |
張偉 | a | 85 | c | 260 |
則a= ，b= ，c= ，d= ，
（2）將90分以上（含90分）的成績視為優秀，則優秀率高的是 .
（3）現在要從這兩個同學選一位去參加數學競賽，你可以根據以上的數據給老師哪些建議？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數y=ax2+bx+c的圖象交x軸于A、B兩點，交y軸于點C，且B（1，0），C（0，3），將△BOC繞點O按逆時針方向旋轉90°，C點恰好與A重合．
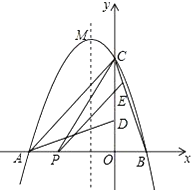
（1）求該二次函數的解析式；
（2）若點P為線段AB上的任一動點，過點P作PE∥AC，交BC于點E，連結CP，求△PCE面積S的最大值；
（3）設拋物線的頂點為M，Q為它的圖象上的任一動點，若△OMQ為以OM為底的等腰三角形，求Q點的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
