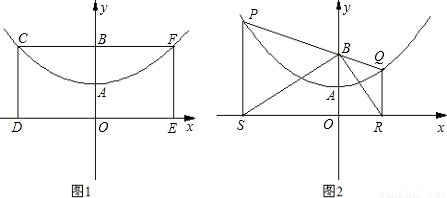
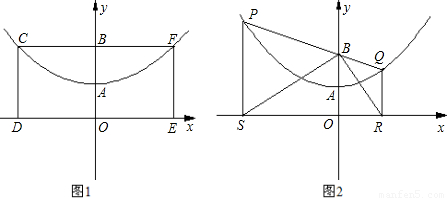
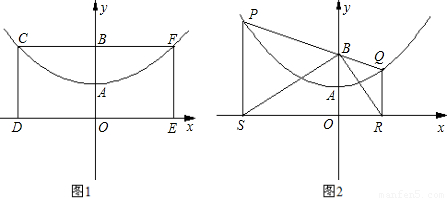
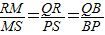【答案】
分析:(1)根據B點的坐標以及矩形的面積可以求出矩形的四個頂點的坐標,根據待定系數法就可以求出拋物線的解析式;
(2)①過點B作BN⊥PS,垂足為N,可以設P的坐標是(a,

a
2+1),根據勾股定理就可以用a表示出PB=PS的長,由此可以證明;
②判斷△SBR的形狀,根據①同理可知BQ=QR,根據等邊對等角就可以證明∠SBR=90度,則△SBR為直角三角形;
③若以P、S、M為頂點的三角形與以Q、M、R為頂點的三角形相似,有△PSM∽△MRQ和△PSM∽△QRM兩種情況,根據相似三角形的對應邊的比相等就可以求出.
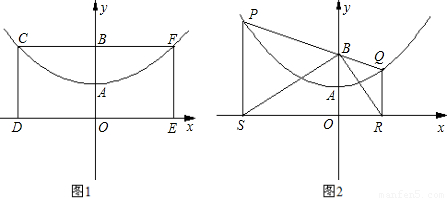
解答:解:(1)方法一:
∵B點坐標為(0.2),
∴OB=2,
∵矩形CDEF面積為8,
∴CF=4.
∴C點坐標為(-2,2).F點坐標為(2,2).
設拋物線的解析式為y=ax
2+bx+c.
其過三點A(0,1),C(-2.2),F(2,2).
得
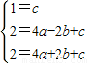
,
解這個方程組,得a=

,b=0,c=1,
∴此拋物線的解析式為y=

x
2+1.(3分)
方法二:
∵B點坐標為(0.2),
∴OB=2,
∵矩形CDEF面積為8,
∴CF=4.
∴C點坐標為(-2,2),
根據題意可設拋物線解析式為y=ax
2+c.
其過點A(0,1)和C(-2.2)
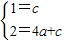
解這個方程組,得a=

,c=1
此拋物線解析式為y=

x
2+1.
(2)①證明:如圖(2)過點B作BN⊥PS,垂足為N.
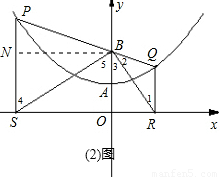
∵P點在拋物線y=

x
2+1上.可設P點坐標為(a,

a
2+1).
∴PS=

a
2+1,OB=NS=2,BN=-a.
∴PN=PS-NS=
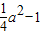
,
在Rt△PNB中.
PB
2=PN
2+BN
2=(

a
2-1)
2+a
2=(

a
2+1)
2∴PB=PS=
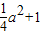
.(6分)
②根據①同理可知BQ=QR.
∴∠1=∠2,
又∵∠1=∠3,
∴∠2=∠3,
同理∠SBP=∠5(7分)
∴2∠5+2∠3=180°
∴∠5+∠3=90°
∴∠SBR=90度.
∴△SBR為直角三角形.(8分)
③方法一:如圖(3)作QN⊥PS,
設PS=b,QR=c,
∵由①知PS=PB=b.QR=QB=c,PQ=b+c.PN=b-c.
∴QN
2=SR
2=(b+c)
2-(b-c)
2∴
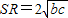
.(9分)
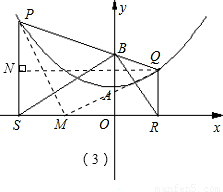
假設存在點M.且MS=x,則MR=
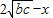
.
若使△PSM∽△MRQ,
則有
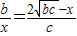
.
即x
2-2
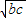
x+bc=0
∴

.
∴SR=2
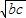
∴M為SR的中點.(11分)
若使△PSM∽△QRM,
則有
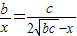
.
∴
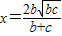
.
∴
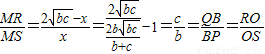
.
∴M點即為原點O.
綜上所述,當點M為SR的中點時.△PSM∽△MRQ;
當點M為原點時,△PSM∽△MRQ.(13分)
方法二:
若以P、S、M為頂點的三角形與以Q、M、R為頂點的三角形相似,
∵∠PSM=∠MRQ=90°,
∴有△PSM∽△MRQ和△PSM∽△QRM兩種情況.
當△PSM∽△MRQ時.∠SPM=∠RMQ,∠SMP=∠RQM.
由直角三角形兩銳角互余性質.知∠PMS+∠QMR=90度.
∴∠PMQ=90度.(9分)
取PQ中點為T.連接MT.則MT=

PQ=

(QR+PS).(10分)
∴MN為直角梯形SRQP的中位線,
∴點M為SR的中點(11分)
∴
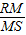
=1
當△PSM∽△QRM時,
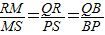
∴QB=BP
∵PS∥OB∥QR
∴點M為原點O.
綜上所述,當點M為SR的中點時,△PSM∽△MRQ;
當點M為原點時,△PSM∽△QRM.(13分)
點評:本題主要考查了待定系數法求函數解析式,以及相似三角形的對應邊的比相等.

 a2+1),根據勾股定理就可以用a表示出PB=PS的長,由此可以證明;
a2+1),根據勾股定理就可以用a表示出PB=PS的長,由此可以證明;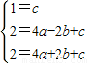 ,
, ,b=0,c=1,
,b=0,c=1, x2+1.(3分)
x2+1.(3分)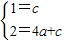
 ,c=1
,c=1 x2+1.
x2+1.
 x2+1上.可設P點坐標為(a,
x2+1上.可設P點坐標為(a, a2+1).
a2+1). a2+1,OB=NS=2,BN=-a.
a2+1,OB=NS=2,BN=-a.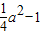 ,
, a2-1)2+a2=(
a2-1)2+a2=( a2+1)2
a2+1)2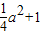 .(6分)
.(6分)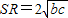 .(9分)
.(9分)
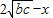 .
.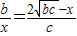 .
.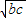 x+bc=0
x+bc=0 .
.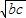
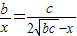 .
.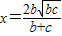 .
.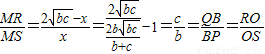 .
. PQ=
PQ= (QR+PS).(10分)
(QR+PS).(10分)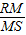 =1
=1