
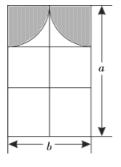
【題目】裝修公司給小紅家的窗戶設計了如圖所示的裝修方案,上方布料窗眉(陰影部分)由兩個半徑相同的四分之一圓組成.
(1)分別用整式表示窗眉用布和窗戶透光的面積.(窗框的面積忽略不計).
(2)觀察(1)中的結果,它們是單項式還是多項式?次數分別是多少?
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,點C在線段![]() 上.點P從點C出發向點
上.點P從點C出發向點![]() 運動,速度為2cm/s;同時,點Q也從點C以4cm/s速度出發用1s到達A處,并在A處停留2s,然后按原速度向點B運動,.最終,點Q比點P早1s到達B處.設點P運動的時間為t.
運動,速度為2cm/s;同時,點Q也從點C以4cm/s速度出發用1s到達A處,并在A處停留2s,然后按原速度向點B運動,.最終,點Q比點P早1s到達B處.設點P運動的時間為t.
(1)線段AC的長為 cm;當t=3s時,P,Q兩點之間的距離為 cm;
(2)求線段BC的長;
(3)從P,Q兩點同時出發至點P到達點B處的這段時間內,t為何值時,P,Q兩點相距1cm?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,長方形ABCD的頂點B在坐標原點,頂點A、C分別在y軸、x軸的負半軸上,其中![]() ,
,![]() ,將矩形ABCD繞點D逆時針旋轉得到矩形
,將矩形ABCD繞點D逆時針旋轉得到矩形![]() ,點
,點![]() 恰好落在x軸上,線段
恰好落在x軸上,線段![]() 與CD交于點E,那么點E的坐標為
與CD交于點E,那么點E的坐標為![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克為標準,超過的千克數記作正數,不足的千克數記作負數,稱后的記錄如下:
千克為標準,超過的千克數記作正數,不足的千克數記作負數,稱后的記錄如下:

![]() 這
這![]() 筐白菜中,最接近
筐白菜中,最接近![]() 千克的那筐白菜為 千克
千克的那筐白菜為 千克
![]() 這
這![]() 筐白菜中,最重的那筐與最輕的那筐相差 千克
筐白菜中,最重的那筐與最輕的那筐相差 千克
![]() 若白菜每千克售價
若白菜每千克售價![]() 元,則這些白菜可賣多少錢?
元,則這些白菜可賣多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】試題分析:把原式的第一項根據負整數指數冪的意義化簡,第二項根據算術平方根的定義求出9的算術平方根,第三項根據零指數公式化簡,最后一項利用特殊角的三角函數值化簡,合并后即可求出值.
試題解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【題型】解答題
【結束】
16
【題目】《九章算術》“勾股”章有一題:“今有二人同所立,甲行率七,乙行率三.乙東行,甲南行十步而斜東北與乙會.問甲乙行各幾何”.大意是說,已知甲、乙二人同時從同一地
點出發,甲的速度為7,乙的速度為3.乙一直向東走,甲先向南走10步,后又斜向北偏東方向走了一段后與乙相遇.那么相遇時,甲、乙各走了多遠?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅行社推出一條成本價為500元/人的省內旅游線路.游客人數![]() (人/月)與旅游報價
(人/月)與旅游報價![]() (元/人)之間的關系為
(元/人)之間的關系為![]() ,已知:旅游主管部門規定該旅游線路報價在800元/人~1200元/人之間.
,已知:旅游主管部門規定該旅游線路報價在800元/人~1200元/人之間.
(1)要將該旅游線路每月游客人數控制在200人以內,求該旅游線路報價的取值范圍;
(2)求經營這條旅游線路每月所需要的最低成本;
(3)當這條旅游線路的旅游報價為多少時,可獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅行社推出一條成本價位500元/人的省內旅游線路,游客人數y(人/月)與旅游報價x(元/人)之間的關系為y=﹣x+1300,已知:旅游主管部門規定該旅游線路報價在800元/人~1200元/人之間.
(1)要將該旅游線路每月游客人數控制在200人以內,求該旅游線路報價的取值范圍;
(2)求經營這條旅游線路每月所需要的最低成本;
(3)檔這條旅游線路的旅游報價為多少時,可獲得最大利潤?最大利潤是多少?
【答案】(1)取值范圍為1100元/人~1200元/人之間;(2)50000;(3)x=900時,w最大=160000
【解析】試題分析:(1)根據題意列不等式求解可;
(2)根據報價減去成本可得到函數的解析式,根據一次函數的圖像求解即可;
(3)根據利潤等于人次乘以價格即可得到函數的解析式,然后根據二次函數的最值求解即可.
試題解析:(1)∵由題意得![]() 時,即
時,即![]() ,
,
∴解得![]()
即要將該旅游線路每月游客人數控制在200人以內,該旅游線路報價的取值范圍為1100元/人~1200元/人之間;
(2)![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴當
,∴當![]() 時,z最低,即
時,z最低,即![]() ;
;
(3)利潤![]()
當![]() 時,
時,![]() .
.
【題型】解答題
【結束】
23
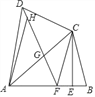
【題目】已知四邊形ABCD中,AB=AD,對角線AC平分∠DAB,過點C作CE⊥AB于點E,點F為AB上一點,且EF=EB,連接DF.
(1)求證:CD=CF;
(2)連接DF,交AC于點G,求證:△DGC∽△ADC;
(3)若點H為線段DG上一點,連接AH,若∠ADC=2∠HAG,AD=3,DC=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
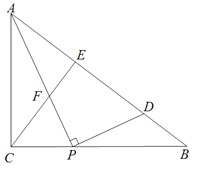
【題目】如圖,已知△ABC中,∠ACB=90°,AC=15,BC=20.動點P在線段CB上,以1cm/s的速度從點C向B運動,連接AP,作CE⊥AB分別交AP、AB于點F、E,過點P作PD⊥AP交AB于點D.
(1)線段CE= ;
(2)若t=5時,求證:△BPD≌△ACF;
(3)t為何值時,△PDB是等腰三角形;
(4)求D點經過的路徑長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com